Page 93 - chapter 1

93
ΚΕΦΑΛΑΙΟ 1 - Όρια - Συνέχεια Συνάρτησης

ΟΡΙΣΜΟΣ
Για μία συνάρτηση f με πεδίο ορισμού Α θα λέμε οτι:
● Παρουσιαζει στο x 0 A (ολικό) μ έ γ ι σ τ ο , το f(x 0), αν

ισχύει:
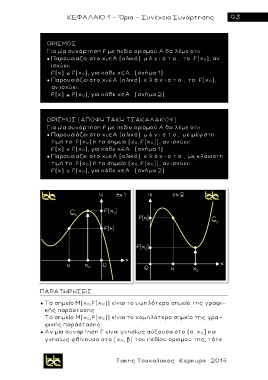
f(x) f(x 0), για κάθε x A (σχήμα 1)
● Παρουσιάζει στο x 0 A (ολικό) ε λ ά χ ι σ τ ο , το f(x 0),
αν ισχύει:
f(x) f(x 0), για κάθε x A (σχήμα 2)

ΟΡΙΣΜΟΣ (ΑΠΟΨΗ ΤΑΚΗ ΤΣΑΚΑΛΑΚΟΥ)
Για μία συνάρτηση f με πεδίο ορισμού Α θα λέμε οτι:
● Παρουσιάζει στο x 0 A (ολικό) μ έ γ ι σ τ ο , με μέγιστη

τιμή το f(x 0) ή το σημείο (x 0, f(x 0)), αν ισχύει:
f(x) f(x 0), για κάθε x A (σχήμα 1)
● Παρουσιαζει στο x 0 A (ολικό) ε λ ά χ ι σ τ ο , με ελάχιστη
τιμή το f(x 0) ή το σημείο (x 0, f(x 0)), αν ισχύει:
f(x) f(x 0), για κάθε x A (σχήμα 2)

ΠΑΡΑΤΗΡΗΣΕΙΣ

● Το σημείο Μ ( x 0,f(x 0)) είναι το υψηλότερο σημείο της γραφι-

κής παράστασης

Το σημείο Μ ( x 0,f(x 0)) είναι το χαμηλότερο σημείο της γ ρ α-

φικής παράστασης

● Αν μία συνάρτηση f είναι γνησίως αύξουσα στο (α, χ 0] και

γνησίως φθίνουσα στο [χ 0, β) του πεδίου ορισμού της, τότε

Τακης Τσακαλακος Κερκυρα 2017