Page 90 - chapter 1

90
ΚΕΦΑΛΑΙΟ 1 - Όρια - Συνέχεια Συνάρτησης

άτοπο,

άρα η C f τέμνει την ευθεία y=α σε ένα το πολύ σημείο.
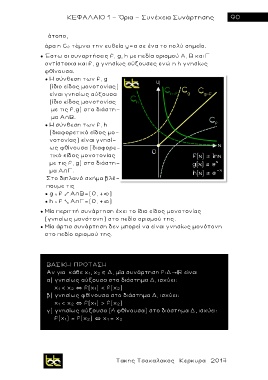
● Έστω οι συναρτήσεις f, g, h με πεδία ορισμού Α, Β και Γ

αντίστοιχα και f, g γνησίως αύξουσες ενώ η h γνησίως
φθίνουσα.
● Η σύνθεση των f, g
(ίδιο είδος μονοτονίας)
είναι γνησίως αύξουσα
(ίδιο είδος μον ο τονίας
με τις f,g) στο διάστη-

μα Α Β.
● Η σύνθεση των f, h
(διαφορετικό είδος μο-
νοτονίας) είναι γνησί-
ω ς φθίνουσα (διαφορ ε -
τικό είδος μονοτονίας
με τις f, g) στο διάστη-
μ α Α Γ.
Στο διπλανό σχήμα βλέ-
πουμε τις

● g ο f е Α Β=(0, + )
● h ο f д Α Γ=(0, + )

● Μία περιττή συνάρτηση έχει το ίδιο είδος μονοτονίας
(γνησίως μονότονη) στο πεδίο ορισμού της.
● Μία άρτια συνάρτηση δεν μπορεί να είναι γνησίως μονότονη
στο πεδίο ορισμ ο ύ της.

ΒΑΣΙΚΗ ΠΡΟΤΑΣΗ
Αν για κάθε χ 1, χ 2 Δ, μία συνάρτηση f: Δ είναι

α) γνησίως αύξουσα στο διάστημα Δ, ισχύει:
χ 1 < χ 2 ` f(χ 1) < f(χ 2)
β) γνησίως φθίνουσα στο διάστημα Δ, ισχύει:

χ 1 < χ 2 ` f(χ 1) > f(χ 2)
γ) γνησίως αύξουσα (ή φθίνουσα) στο διάστημα Δ, ισχύει:
f(χ 1) = f(χ 2) ` χ 1 = χ 2

Τακης Τσακαλακος Κερκυρα 2017