Page 87 - chapter 1

87
ΚΕΦΑΛΑΙΟ 1 - Όρια - Συνέχεια Συνάρτησης

Θ Ε Ω Ρ Ι Α ...

ΟΡΙΣΜΟΣ
Μία συνάρτηση f λέγεται
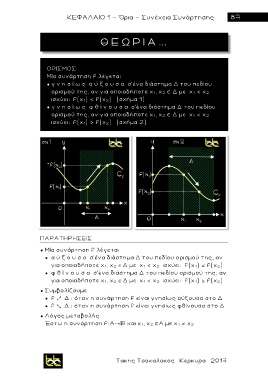
● γ ν η σ ί ω ς α ύ ξ ο υ σ α σ’ένα δ ι άσ τ ημα Δ του πεδίου
ορισμού της, αν για οποιαδήποτε x 1, x 2 Δ με x 1 < x 2
ισχύει: f(x 1) < f(x 2) (σχήμα 1)
● γ ν η σ ί ω ς φ θ ί ν ο υ σ α σ ’ ένα διάστημα Δ του πεδίου
ορισμού της, αν για οποιαδήποτε x 1, x 2 Δ με x 1 < x 2
ισχύει: f(x 1) > f(x 2) (σχήμα 2)

ΠΑΡΑΤΗΡΗΣΕΙΣ

● Μία συνάρτηση f λέγεται

● α ύ ξ ο υ σ α σ’ένα δ ι άστημα Δ του πεδίου ορισμού της, αν
για οποιαδήποτε x 1, x 2 ∈ Δ με x 1 < x 2 ισχύει: f(x 1) f(x 2)

● φ θ ί ν ο υ σ α σ’ένα δ ι άστημα Δ του πεδίου ορισμού της, αν

για οποιαδήποτε x 1, x 2 ∈ Δ με x 1 < x 2 ισχύει: f(x 1) f(x 2)

● Συμβολίζουμε
● f е Δ : όταν η συνάρτηση f είναι γνησίως αύξουσα στο Δ

● f д Δ : όταν η συνάρτηση f είναι γνησίως φθίνουσα στο Δ

● Λόγος μεταβολής
Έστω η συνάρτηση f: Α και x 1, x 2 Α με x 1 x 2

Τακης Τσακαλακος Κερκυρα 2017