Page 5 - olokliroma

5
ΚΕΦΑΛΑΙΟ 3 - Ολοκληρωτικός Λογισμός

Θ Ε Ω Ρ Ι Α ...

ΟΡΙΣΜΟΣ
Έστω μια συνάρτηση f ορισμένη στο διάστημα Δ.
Ονομάζουμε α ρ χ ι κ ή σ υ ν ά ρ τ η σ η ή π α ρ ά γ ο υ σ α
της f στο Δ, κάθε συνάρτηση F που είναι παραγωγίσιμη στο
Δ και ισχύει:
F’(x) = f(x), για κάθε x Δ .

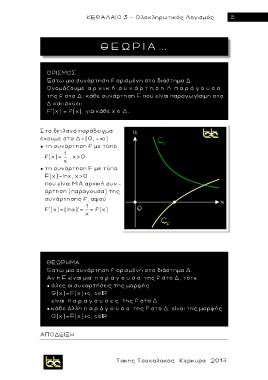
Στο διπλανό παράδειγμα

έχουμε στο Δ=(0, + )
● τη συνάρτηση f με τύπο

1
f(x)= x , x>0

● τη συνάρτηση F με τύπο

F(x)=lnx, x>0

που είναι ΜΙΑ αρχική συν-

άρτηση (παράγουσα) της
συνάρτησης f, αφού

1
F'(x)=(lnx)'= x = f(x)

ΘΕΩΡΗΜΑ
Έστω μια συνάρτηση f ορισμένη στο διάστημα Δ.

Αν η F είναι μια π α ρ ά γ ο υ σ α της f στο Δ, τότε
● όλες οι συναρτήσεις της μορφής
G(x)=F(x)+c, c
είναι π α ρ ά γ ο υ σ ε ς της f στο Δ

● κάθε άλλη π α ρ ά γ ο υ σ α της f στο Δ είναι της μορφής
G(x)=F(x)+c, c

ΑΠΟΔΕΙΞΗ

Τακης Τσακαλακος Κερκυρα 2017