Page 7 - olokliroma

7
ΚΕΦΑΛΑΙΟ 3 - Ολοκληρωτικός Λογισμός

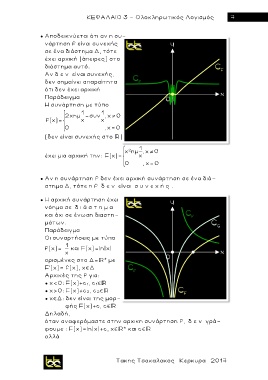
● Αποδεικνύεται ότι αν η συ-
νάρτηση f είναι συνεχής
σε ένα διάστημα Δ, τότε
έχει αρχική (άπειρες) στο

διάστημα αυτό.
Αν δ ε ν είναι συνεχής,
δεν σημαίνει απαραίτητα
ότι δεν έχει αρχική
Παράδειγμα
Η συνάρτηση με τύπο
1 1
2xημ -συν , χ 0
f(x)= χ χ έχει
0 , χ= 0

(δεν είναι συνεχής στο )

1
x ημ , χ 0
2
έχει μια αρχική την: F(x)= χ
0 , χ= 0

● Αν η συνάρτηση f δεν έχει αρχική συνάρτηση σε ένα διά-
στημα Δ, τότε η f δ ε ν είναι σ υ ν ε χ ή ς .

● Η αρχική συνάρτηση έχει
νόημα σε δ ι ά σ τ η μ α
και όχι σε ένωση διαστη-

μάτων.
Παράδειγμα
Ο ι συναρτήσεις με τύπο
1
f(x)= και F(x)=ln|x|
χ
ορισμένες στο Δ= * με
F'(x)= f(x), χ Δ
Αρχικές της f για:

● χ<0: F(x)+c 1, c 1
● χ>0: F(x)+c 2, c 2
● χ Δ: δεν είναι της μορ-
φής F(x)+c, c
Δηλαδή,
όταν αναφερόμαστε στην αρχικη συνάρτηση f, δ ε ν γρά-
φουμε : F(x)=ln|x|+c, x * και c
αλλά

Τακης Τσακαλακος Κερκυρα 2017