Page 12 - E Book Turunan dan Aplikasinya (Matematika Wajib XI)
P. 12
B A B 7 | m a t e m a t i k a w a j I b X I | s e m e s t e r I V
F. APLIKASI TURUNAN UNTUK MENENTUKAN TITIK STATIONER
Setiap fungsi pasti memiliki yang namanya titik balik, baik maksimum (puncak) maupun titik
minimum (lembah) dan titik belok. Kumpulan semua titik balik dan titik belok disebut dengan
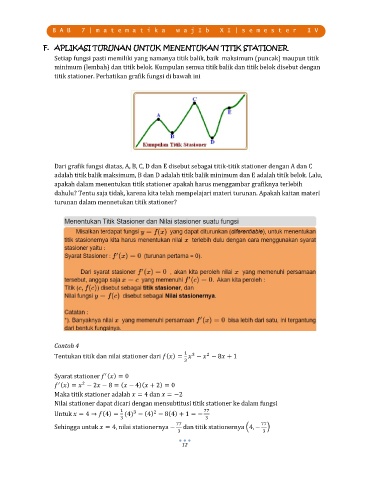
titik stationer. Perhatikan grafik fungsi di bawah ini
Dari grafik fungsi diatas, A, B, C, D dan E disebut sebagai titik-titik stationer dengan A dan C
adalah titik balik maksimum, B dan D adalah titik balik minimum dan E adalah titik belok. Lalu,
apakah dalam menentukan titik stationer apakah harus menggambar grafiknya terlebih
dahulu? Tentu saja tidak, karena kita telah mempelajari materi turunan. Apakah kaitan materi
turunan dalam mennetukan titik stationer?
Contoh 4
Tentukan titik dan nilai stationer dari =
Syarat stationer =
= = =
Maka titik stationer adalah = dan =
Nilai stationer dapat dicari dengan mensubtitusi titik stationer ke dalam fungsi
Untuk = → = =
Sehingga untuk = , nilai stationernya dan titik stationernya ( )
12