Page 166 - Maxwell House

146 Chapter 3

Table 3.1

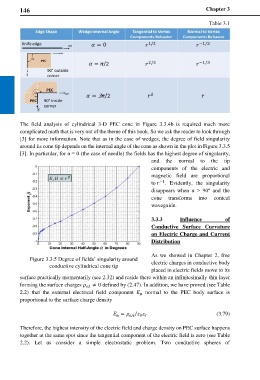
The field analysis of cylindrical 3-D PEC cone in Figure 3.3.4b is required much more
complicated math that is very out of the theme of this book. So we ask the reader to look through
[3] for more information. Note that as in the case of wedges, the degree of field singularity
around its cone tip depends on the internal angle of the cone as shown in the plot in Figure 3.3.5
[3]. In particular, for α = 0 (the case of needle) the fields has the highest degree of singularity,
and the normal to the tip
components of the electric and
magnetic field are proportional
to −1 . Evidently, the singularity
disappears when α > 90° and the
cone transforms into conical
waveguide.

3.3.3 Influence of
Conductive Surface Curvature
on Electric Charge and Current
Distribution

As we showed in Chapter 2, free
Figure 3.3.5 Degree of fields’ singularity around electric charges in conductive body
conductive cylindrical cone tip
placed in electric fields move to its
surface practically momentarily (see 2.32) and reside there within an infinitesimally thin layer
forming the surface charges ≠ 0 defined by (2.47). In addition, we have proved (see Table
2.2) that the external electrical field component normal to the PEC body surface is

proportional to the surface charge density

= ⁄ (3.79)

0
Therefore, the highest intensity of the electric field and charge density on PEC surface happens
together at the same spot since the tangential component of the electric field is zero (see Table
2.2). Let us consider a simple electrostatic problem. Two conductive spheres of