Page 29 - Maxwell House

BASIC EQUATIONS OF MACROSCOPIC ELECTRODYNAMICS 9

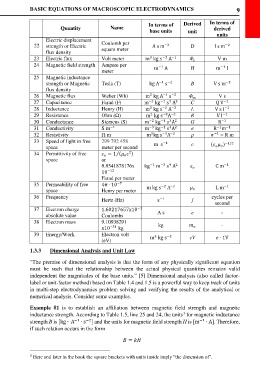
Quantity Name In terms of Derived In terms of
derived
base units
unit
Electric displacement units
22 strength or Electric Coulomb per A s m D I s m
−2
−2
flux density square meter
23 Electric flux Volt meter m kg A V m
−1
3
−3
24 Magnetic field strength Ampere per
−1
−1
meter m A H m I
25 Magnetic inductance
strength or Magnetic Tesla (T) kg A s B V s m
−1
−2
−2
flux density
26 Magnetic flux Weber (Wb) m kg A s V s
−1
2
−2
27 Capacitance Farad (F) m kg s A C Q V
2
−1
−1
−2
4
28 Inductance Henry (H) m kg s A L V s I
−2
−2
2
−1
29 Resistance Ohm (Ω) m kg s A R V I
−3 −2
−1
2
30 Conductance Siemens (S) m kg s A G R
−1
−1
3 2
−2
31 Conductivity S m m kg s A σ R m
−1
−3
3 2
−1
−1
−1
32 Resistivity Ω m m kg s A = R m
−3 −2
−1
2
33 Speed of light in free 299 792 458
−1
space meter per second m s c ( 0 ) −1/2
34 Permittivity of free = 1 ( 0 c )
2
⁄
space or
8.8541878176x kg m s A C m
−1
2
−1
−3
4
10 −12
Farad per meter
35 Permeability of free 4π ∙ 10
−7
−2
−2
−1
space Henry per meter m kg s A 0 L m
36 Frequency Hertz (Hz) s f cycles per
−1
second
37 Electron charge 1.60217657x10 −1
absolute value Coulombs A s e -
38 Electron mass 9.10938291 kg -
x10 −31 kg
39 Energy/Work Electron volt
2
−2
(eV) m kg s eV ∙ 1V
1.3.3 Dimensional Analysis and Unit Law
“The premise of dimensional analysis is that the form of any physically significant equation
must be such that the relationship between the actual physical quantities remains valid
independent the magnitudes of the base units.” [5] Dimensional analysis (also called factor-
label or unit-factor method) based on Table 1.4 and 1.5 is a powerful way to keep track of units
in multi-step electrodynamics problem solving and verifying the results of the analytical or
numerical analysis. Consider some examples.
Example #1 is to establish an affiliation between magnetic field strength and magnetic
3
inductance strength. According to Table 1.5, line 25 and 24, the units for magnetic inductance
−1 −2 −1 ∙ A]. Therefore,
strength B is [kg ∙ A ∙ s ] and the units for magnetic field strength H is [m
if such relation occurs in the form
=
3 Here and later in the book the square brackets with units inside imply “the dimension of”.