Page 328 - Maxwell House

308 Chapter 6

of (6.29) and (6.30) postponing the numerical one until the next section. Note only again that
analytical solution could be actually found for quite restricted number of line geometries. For
example, this group includes a coaxial cable, rectangular, circular of elliptical waveguides and
some others where the boundaries coincide with orthogonal coordinate lines.

6.6 MORE INFORMATION ABOUT FEED LINES

6.6.1 Introduction
The most data in this section are the results of numerical simulations based on MATLAB code
®
and CST STUDIO SUITE software. We hope that this set of field patterns and plots of feed
characteristics can help our reader better navigate the numerical simulation process and would
serve as the first of the design steps in some applications.
6.6.2 Two-Wire Line

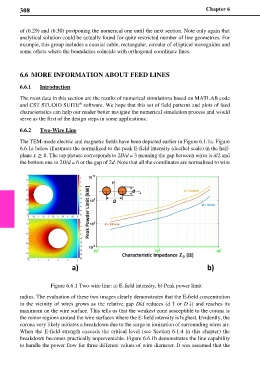
The TEM-mode electric and magnetic fields have been depicted earlier in Figure 6.1.1a. Figure
6.6.1a below illustrates the normalized to the peak E-field intensity (decibel scale) in the half-
plane ≥ 0. The top picture corresponds to 2D/d = 3 meaning the gap between wires is d/2 and
the bottom one to 2D/d = 6 or the gap of 2d. Note that all the coordinates are normalized to wire

a) b)

Figure 6.6.1 Two-wire line: a) E-field intensity, b) Peak power limit

radius. The evaluation of these two images clearly demonstrates that the E-field concentration

in the vicinity of wires grows as the relative gap D/d reduces (d ↑ or D ↓) and reaches its
maximum on the wire surface. This tells us that the weakest zone susceptible to the corona is
the minor regions around the wire surfaces where the E-field intensity is highest. Evidently, the
corona very likely initiates a breakdown due to the surge in ionization of surrounding wires air.
When the E-field strength exceeds the critical level (see Section 6.1.4 in this chapter) the
breakdown becomes practically unpreventable. Figure 6.6.1b demonstrates the line capability
to handle the power flow for three different values of wire diameter. It was assumed that the