Page 329 - Maxwell House

FEED LINE BASICS 309

line is surrounded by dry air on the sea level at 20℃ while the electrical breakdown field
strength is 3 MV/m. It is advisable to use in practice the values approximately tenfold below
taking into consideration the harsh environment of open space. According to graphs in Figure
6.6.1b, the ability of the two-wire line to carry high electric power is in the range of hundreds
of MW. That is why different modifications of such line like shown in Figure 6.2.1 are widely
used as overhead power lines to deliver and distribute AC electrical energy along long
distances. Since the operating voltage in such lines reaches 1 MV, the line wires should be
separated quite extensively creating thereby the large field radius as Figure 6.1.1b illustrates.

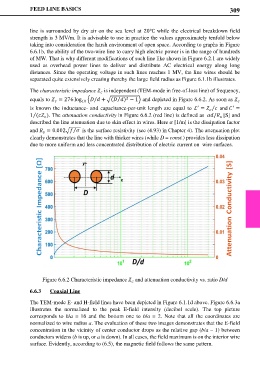
The characteristic impedance is independent (TEM-mode in free-of-loss line) of frequency,

2
equals to = 276 log 10 �/ + �( ) − 1� and depicted in Figure 6.6.2. As soon as
⁄

′
′
⁄
is known the inductance- and capacitance-per-unit length are equal to ℒ = and =

1 ( ). The attenuation conductivity in Figure 6.6.2 (red line) is defined as / [S] and
⁄

described the line attenuation due to skin effect in wires. Here [1/m] is the dissipation factor
and = 0.002� is the surface resistivity (see (4.93) in Chapter 4). The attenuation plot
⁄

clearly demonstrates that the line with thicker wires (while D = const.) provides less dissipation
due to more uniform and less concentrated distribution of electric current on wire surfaces.

Figure 6.6.2 Characteristic impedance and attenuation conductivity vs. ratio D/d

6.6.3 Coaxial Line
The TEM-mode E- and H-field lines have been depicted in Figure 6.1.1d above. Figure 6.6.3a
illustrates the normalized to the peak E-field intensity (decibel scale). The top picture
corresponds to b/a = 16 and the bottom one to b/a = 2. Note that all the coordinates are
normalized to wire radius a. The evaluation of these two images demonstrates that the E-field
concentration in the vicinity of center conductor drops as the relative gap (b/a – 1) between
conductors widens (b is up, or a is down). In all cases, the field maximum is on the interior wire
surface. Evidently, according to (6.5), the magnetic field follows the same pattern.