Page 330 - Maxwell House

310 Chapter 6

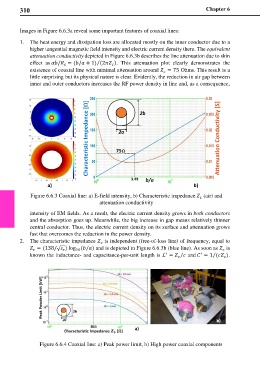
Images in Figure 6.6.3a reveal some important features of coaxial lines:
1. The heat energy and dissipation loss are allocated mostly on the inner conductor due to a
higher tangential magnetic field intensity and electric current density there. The equivalent
attenuation conductivity depicted in Figure 6.6.3b describes the line attenuation due to skin
effect as / = (/ + 1) (2 )⁄ . This attenuation plot clearly demonstrates the

existence of coaxial line with minimal attenuation around = 75 Ohms. This result is a

little surprising but its physical nature is clear. Evidently, the reduction in air gap between
inner and outer conductors increases the RF power density in line and, as a consequence,

Characteristic Impedance [Ω] 75Ω 2b Attenuation Conductivity [S]

2a

3.49 b/a
a) b)
Figure 6.6.3 Coaxial line: a) E-field intensity, b) Characteristic impedance (air) and

attenuation conductivity
intensity of EM fields. As a result, the electric current density grows in both conductors
and the absorption goes up. Meanwhile, the big increase in gap means relatively thinner
central conductor. Thus, the electric current density on its surface and attenuation grows
fast that overcomes the reduction in the power density.
2. The characteristic impedance is independent (free-of-loss line) of frequency, equal to

= (138/ √ ) log (/) and is depicted in Figure 6.6.3b (blue line). As soon as is

10

known the inductance- and capacitance-per-unit length is ℒ = and = 1 ( ).
′
′
⁄
⁄

b)
a)

Figure 6.6.4 Coaxial line: a) Peak power limit, b) High power coaxial components