Page 132 - Servo Motors and Industrial Control Theory -

7.5 A Numerical Investigation of the Transient Behavior … 127

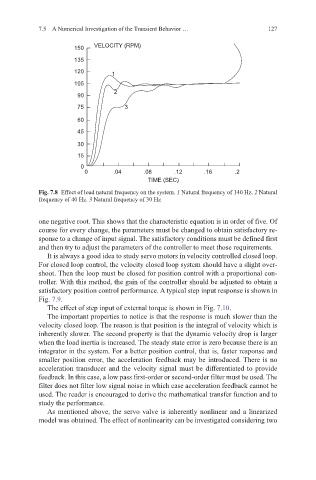
150 VELOCITY (RPM)

135
120 1
105
2
90
75 3
60
45
30
15
0
0 .04 .08 .12 .16 .2
TIME (SEC)

Fig. 7.8 Effect of load natural frequency on the system. 1 Natural frequency of 140 Hz. 2 Natural
frequency of 40 Hz. 3 Natural frequency of 30 Hz

one negative root. This shows that the characteristic equation is in order of five. Of
course for every change, the parameters must be changed to obtain satisfactory re-
sponse to a change of input signal. The satisfactory conditions must be defined first
and then try to adjust the parameters of the controller to meet those requirements.
It is always a good idea to study servo motors in velocity controlled closed loop.
For closed loop control, the velocity closed loop system should have a slight over-
shoot. Then the loop must be closed for position control with a proportional con-
troller. With this method, the gain of the controller should be adjusted to obtain a
satisfactory position control performance. A typical step input response is shown in
Fig. 7.9.
The effect of step input of external torque is shown in Fig. 7.10.
The important properties to notice is that the response is much slower than the
velocity closed loop. The reason is that position is the integral of velocity which is
inherently slower. The second property is that the dynamic velocity drop is larger
when the load inertia is increased. The steady state error is zero because there is an
integrator in the system. For a better position control, that is, faster response and
smaller position error, the acceleration feedback may be introduced. There is no
acceleration transducer and the velocity signal must be differentiated to provide
feedback. In this case, a low pass first-order or second-order filter must be used. The
filter does not filter low signal noise in which case acceleration feedback cannot be
used. The reader is encouraged to derive the mathematical transfer function and to
study the performance.
As mentioned above, the servo valve is inherently nonlinear and a linearized
model was obtained. The effect of nonlinearity can be investigated considering two