Page 134 - Servo Motors and Industrial Control Theory -

7.6 Conclusion 129

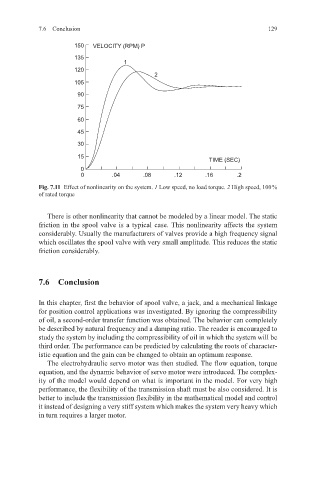
150 VELOCITY (RPM) P
135
1
120
2
105
90
75
60
45
30
15
TIME (SEC)
0
0 .04 .08 .12 .16 .2
Fig. 7.11 Effect of nonlinearity on the system. 1 Low speed, no load torque. 2 High speed, 100 %
of rated torque

There is other nonlinearity that cannot be modeled by a linear model. The static
friction in the spool valve is a typical case. This nonlinearity affects the system
considerably. Usually the manufacturers of valves provide a high frequency signal
which oscillates the spool valve with very small amplitude. This reduces the static
friction considerably.

7.6 Conclusion

In this chapter, first the behavior of spool valve, a jack, and a mechanical linkage
for position control applications was investigated. By ignoring the compressibility
of oil, a second-order transfer function was obtained. The behavior can completely
be described by natural frequency and a damping ratio. The reader is encouraged to
study the system by including the compressibility of oil in which the system will be
third order. The performance can be predicted by calculating the roots of character-
istic equation and the gain can be changed to obtain an optimum response.
The electrohydraulic servo motor was then studied. The flow equation, torque
equation, and the dynamic behavior of servo motor were introduced. The complex-
ity of the model would depend on what is important in the model. For very high
performance, the flexibility of the transmission shaft must be also considered. It is
better to include the transmission flexibility in the mathematical model and control
it instead of designing a very stiff system which makes the system very heavy which
in turn requires a larger motor.