Page 22 - Fisika Kelas XI CP Terbaru

Panjang vektor resultan dapat diukur dengan mistar dan arah resultan
dapat diukur menggunakan busur derajat.
R = F 1 + F 2
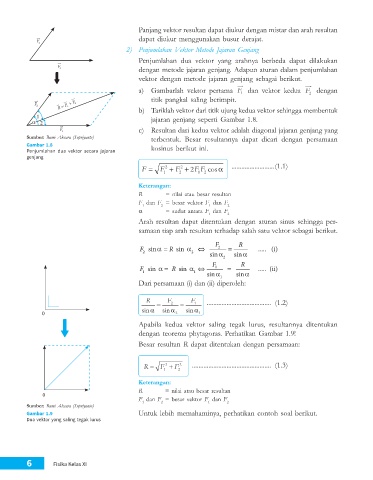
2) Penjumlahan Vektor Metode Jajaran Genjang
Penjumlahan dua vektor yang arahnya berbeda dapat dilakukan

R = F 1 + F 2 dengan metode jajaran genjang. Adapun aturan dalam penjumlahan
vektor dengan metode jajaran genjang sebagai berikut.

a) Gambarlah vektor pertama F dan vektor kedua F dengan
1
2
F titik pangkal saling berimpit.
R = F 1 + F 2 F + 2
R = 1 b) Tariklah vektor dari titik ujung kedua vektor sehingga membentuk
1 jajaran genjang seperti Gambar 1.8.
α 2
R = F 1 + F 2 c) Resultan dari kedua vektor adalah diagonal jajaran genjang yang
Sumber: Bumi Aksara (Supriyanto) terbentuk. Besar resultannya dapat dicari dengan persamaan
Gambar 1.8 kosinus berikut ini.
Penjumlahan dua vektor secara jajaran
genjang
F = F + F + 2 F F cosα ..........................(1.1)
2
2
12
2
1
Keterangan:
R = nilai atau besar resultan
F dan F = besar vektor F dan F
1 2 1 2
α = sudut antara F dan F 2
1
Arah resultan dapat ditentukan dengan aturan sinus sehingga per-
samaan tiap arah resultan terhadap salah satu vektor sebagai berikut.

F R
F sinα = R sin α ⇔ sinα = sinα ..... (i)
2
2
2
F 2 R
R sin
α
F sin α = α ⇔ 1 = ..... (ii)
1
1
sin α 1 sin α
Dari persamaan (i) dan (ii) diperoleh:
R = F 2 = F 1 ....................................... (1.2)
sinα sinα sinα
0 2 1
Apabila kedua vektor saling tegak lurus, resultannya ditentukan
dengan teorema phytagoras. Perhatikan Gambar 1.9!
Besar resultan R dapat ditentukan dengan persamaan:

R = F + F 2 2 ................................................ (1.3)
2
1
Keterangan:
R = nilai atau besar resultan
0
F dan F = besar vektor F dan F 2
1
2
1
Sumber: Bumi Aksara (Supriyanto)
Gambar 1.9 Untuk lebih memahaminya, perhatikan contoh soal berikut.
Dua vektor yang saling tegak lurus

6 Fisika Kelas XI