Page 33 - Tlahuizcalli CB-31_Neat

experimento para cien, mil, diez mil, cien mil y un En la figura 3 se muestra la distribución de la
millón de casos diferentes, cada uno suma de puntos para una simulación de 100
correspondiente a una jugada. juegos. Al representar un número bajo de
simulaciones no es posible observar una tendencia
De acuerdo a Steen (2000), la variación clara en la distribución de los datos, pero conforme
aleatoria puede investigarse empíricamente se va incrementando el número de simulaciones
aplicando las herramientas del análisis de datos (ver figuras 4, 5, 6, y 7) se evidencia una distribución
para poner de manifiesto la regularidad presente gaussiana. En la figura 7 se ha sobrepuesto una
en los resultados aleatorios. La probabilidad línea de tendencia gaussiana y se muestra que
proporciona los recursos matemáticos que ajusta perfectamente con el histograma.
describen el azar con mucho mayor detalle del
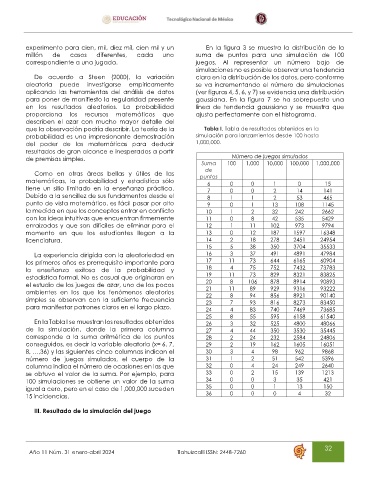
que la observación podría describir. La teoría de la Tabla I. Tabla de resultados obtenidos en la
probabilidad es una impresionante demostración simulación para lanzamientos desde 100 hasta
del poder de las matemáticas para deducir 1,000,000.
resultados de gran alcance e inesperados a partir
de premisas simples. Número de juegos simulados
Suma 100 1,000 10,000 100,000 1,000,000
de
Como en otras áreas bellas y útiles de las
matemáticas, la probabilidad y estadística sólo puntos 0 0 1 0 15
6
tiene un sitio limitado en la enseñanza práctica. 7 0 0 2 14 141
Debido a la sencillez de sus fundamentos desde el 8 1 1 2 53 465
punto de vista matemático, es fácil pasar por alto 9 0 1 13 108 1145
la medida en que los conceptos entrar en conflicto 10 1 2 32 242 2662
con las ideas intuitivas que encuentran firmemente 11 0 8 42 535 5429
enraizadas y que son difíciles de eliminar para el 12 1 11 102 973 9794
momento en que los estudiantes llegan a la 13 0 12 187 1597 16348
licenciatura. 14 2 18 278 2451 24954
15 5 38 350 3704 35533
La experiencia dirigida con la aleatoriedad en 16 3 37 491 4891 47984
los primeros años es prerrequisito importante para 17 11 73 644 6165 60904
la enseñanza exitosa de la probabilidad y 18 4 75 752 7432 73783
estadística formal. No es casual que originaran en 19 11 73 829 8321 83825
8
el estudio de los juegos de azar, uno de los pocos 20 11 106 878 8914 90893
21
929
9316
93222
89
ambientes en los que los fenómenos aleatorios 22 8 94 856 8921 90140
simples se observan con la suficiente frecuencia 23 7 93 816 8273 83450
para manifestar patrones claros en el largo plazo. 24 4 83 740 7469 73685
25 8 55 595 6158 61540
En la Tabla I se muestran los resultados obtenidos 26 3 32 525 4800 48066
de la simulación, donde la primera columna 27 4 44 350 3530 35445
corresponde a la suma aritmética de los puntos 28 2 24 232 2584 24806
conseguidos, es decir la variable aleatoria (x= 6, 7, 29 2 19 162 1605 16051
8, …,36) y las siguientes cinco columnas indican el 30 3 4 98 962 9868
número de juegos simulados, el cuerpo de la 31 1 2 51 542 5396
columna indica el número de ocasiones en las que 32 0 4 24 249 2640
se obtuvo el valor de la suma. Por ejemplo, para 33 0 2 15 139 1213
100 simulaciones se obtiene un valor de la suma 34 0 0 3 35 421
igual a cero, pero en el caso de 1,000,000 suceden 35 0 0 1 13 150
15 incidencias. 36 0 0 0 4 32

III. Resultado de la simulación del juego

32
Año 11 Núm. 31 enero-abril 2024 Tlahuizcalli ISSN: 2448-7260