Page 16 - Trigonometria 1° Sec GM

Capítulo 7

Sector circular II

ÁREA DEL SECTOR CIRCULAR - FORMULA GENERAL

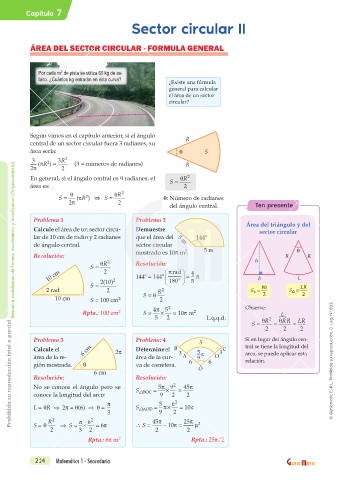
Por cada m de pista se utiliza 60 kg de as-
2
falto. ¿Cuántos kg entrarán en esta curva? ¿Existe una fórmula
general para calcular
el área de un sector
circular?

Según vimos en el capítulo anterior, si el ángulo
central de un sector circular fuera 3 radianes, su R
área sería:  S
3 (pR ) = 3R 2 (3 = números de radianes)
2
Resuelve problemas de forma, movimiento y localización (Trigonometría)
2p 2 R
En general, si el ángulo central es q radianes, el S = R 2
área es: 2
θ θR 2
2
S = (pR )  S = : Número de radianes
2 π 2
del ángulo central. Ten presente
Problema 1 Problema 2
Área del triángulo y del
Calcule el área de un sector circu- Demuestre sector circular
lar de 10 cm de radio y 2 radianes que el área del 5 m 144º
de ángulo central. sector circular
2
mostrado es 10p m . 5 m 
Resolución: R R
θR 2 Resolución: h
S = 2
10 cm 2 144º = 144º   πrad   = 4 p b L
5
180º 
S = 210()  bh LR
2 rad 2 R 2 S  = S =
10 cm S = 100 cm 2 S = q 2 2 2
4π 5 2 Observe:
2
Rpta.: 100 cm 2 S = × = 10p m 
L
5 2 L.q.q.d. θ R 2 θ RR LR
Prohibida su reproducción total o parcia l
S = = =
2 2 2
Problema 3: Problema 4 S Si en lugar del ángulo cen-
Calcule el 6 cm Determine el B 5 3 C tral se tiene la longitud del
área de la re- área de la cur- 3 A 9 D arco, se puede aplicar esta
gión mostrada. va de carretera. 6 6 relación.  Geniomatic E.I.R.L. Prohibida su reproducción. D. Leg. N° 822
6 cm O
Resolución: Resolución:
No se conoce el ángulo pero se S = 5π × 9 2 = 45π
conoce la longitud del arco: BOC 9 2 2
p 5 6 2
L = qR  2p = q(6)  q = S AOD = π× = 10p
3 9 2
R 2 π 6 2 45p 25p
S = q  S = × = 6p  S = – 10p = m 2
2 3 2 2 2
Rpta.: 6p m 2 Rpta.: 25p/2

214 Matemática 1 - Secundaria