Page 77 - PORTAFOLIO SEGUNDO PARCIAL
P. 77
Aplicar los conocimientos adquiridos por medio de ejercicios prácticos tomando en cuenta el
estudio ejecutado.
MÉTODOS DE CÁLCULO DE VOLÚMENES DE REVOLUCIÓN
Método del Disco
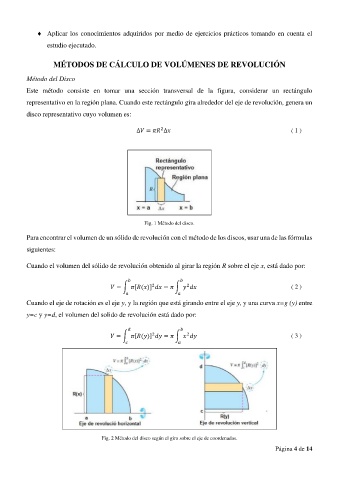
Este método consiste en tomar una sección transversal de la figura, considerar un rectángulo
representativo en la región plana. Cuando este rectángulo gira alrededor del eje de revolución, genera un
disco representativo cuyo volumen es:
2
∆ = ∆ ( 1 )
Fig. 1 Método del disco.
Para encontrar el volumen de un sólido de revolución con el método de los discos, usar una de las fórmulas
siguientes:
Cuando el volumen del sólido de revolución obtenido al girar la región R sobre el eje x, está dado por:
2
2
= ∫ [ ( )] = ∫ ( 2 )
Cuando el eje de rotación es el eje y, y la región que está girando entre el eje y, y una curva x=g (y) entre
y=c y y=d, el volumen del solido de revolución está dado por:
2
2
= ∫ [ ( )] = ∫ ( 3 )
Fig. 2 Método del disco según el giro sobre el eje de coordenadas.
Página 4 de 14