Page 82 - PORTAFOLIO SEGUNDO PARCIAL

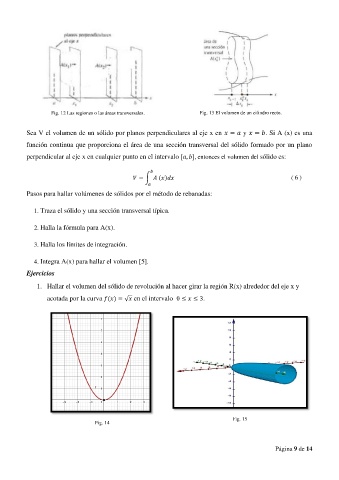
Fig. 12 Las regiones o las áreas transversales. Fig. 13 El volumen de un cilindro recto.

Sea V el volumen de un sólido por planos perpendiculares al eje x en = y = . Si A (x) es una

función continua que proporciona el área de una sección transversal del sólido formado por un plano

perpendicular al eje x en cualquier punto en el intervalo [ , ], entonces el volumen del sólido es:

= ∫ ( ) ( 6 )

Pasos para hallar volúmenes de sólidos por el método de rebanadas:

1. Traza el sólido y una sección transversal típica.

2. Halla la fórmula para A(x).

3. Halla los límites de integración.

4. Integra A(x) para hallar el volumen [5].

Ejercicios

1. Hallar el volumen del sólido de revolución al hacer girar la región R(x) alrededor del eje x y
acotada por la curva ( ) = √ en el intervalo 0 ≤ ≤ 3.

Fig. 14 Fig. 15

Página 9 de 14