Page 79 - PORTAFOLIO SEGUNDO PARCIAL

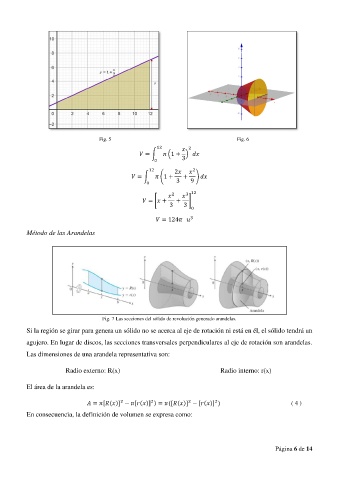
Fig. 5 Fig. 6
12 2
= ∫ (1 + )
0 3
12 2 2
= ∫ (1 + + )
0 3 9
2 3 12
= [ + + ]
3 3
0
3
= 124
Método de las Arandelas

Fig. 7 Las secciones del sólido de revolución generado arandelas.

Si la región se girar para genera un sólido no se acerca al eje de rotación ni está en él, el sólido tendrá un
agujero. En lugar de discos, las secciones transversales perpendiculares al eje de rotación son arandelas.

Las dimensiones de una arandela representativa son:

Radio externo: R(x) Radio interno: r(x)

El área de la arandela es:

2
2
2
2
= [ ( )] − [ ( )] ) = ([ ( )] − [ ( )] ) ( 4 )
En consecuencia, la definición de volumen se expresa como:

Página 6 de 14