Page 80 - PORTAFOLIO SEGUNDO PARCIAL

2
2
= ∫ ( ) = ∫ ([ ( )] − [ ( )] ) ( 5 )

Pasos para hallar volúmenes de sólidos por el método de las arandelas:

1. Dibuja la región y haga el bosquejo de un segmento de recta que la cruce y sea perpendicular al eje de

rotación.

2. Determine los radios exterior e inferior de la arandela que se genera al hacer girar este segmento
alrededor del eje x.

3. Determine los límites de integración determinando las coordenadas x de los puntos de intersección de
la curva y la recta.

4. Evalué la integral del volumen [3].

Ejercicios

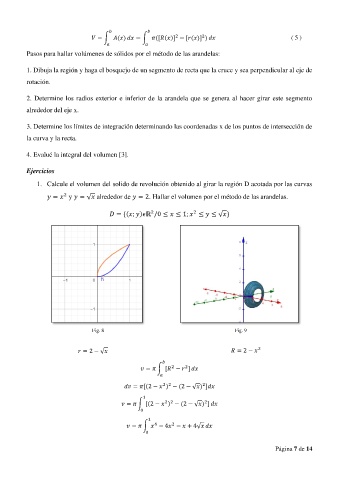
1. Calcule el volumen del solido de revolución obtenido al girar la región D acotada por las curvas
2
= y = √ alrededor de = 2. Hallar el volumen por el método de las arandelas.

2
= {( ; ) ℝ /0 ≤ ≤ 1; ≤ ≤ √ }
2

Fig. 8 Fig. 9

= 2 − √ = 2 − 2

2
2
= ∫ [ − ]

2
2 2
= [(2 − ) − (2 − √ ) ]
1
2 2
2
= ∫ [(2 − ) − (2 − √ ) ]
0
1
2
4
= ∫ − 4 − + 4√
0
Página 7 de 14