Page 81 - PORTAFOLIO SEGUNDO PARCIAL

31
3
=
30
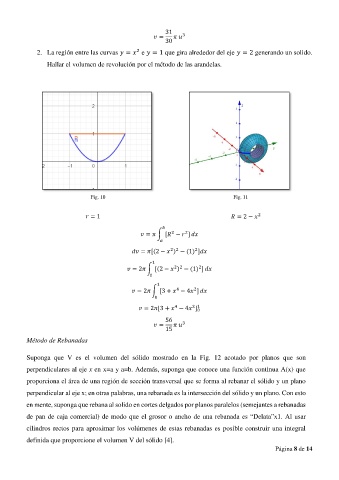
2. La región entre las curvas = e = 1 que gira alrededor del eje = 2 generando un solido.
2
Hallar el volumen de revolución por el método de las arandelas.

Fig. 10 Fig. 11

2
= 1 = 2 −

2
2
= ∫ [ − ]

2 2
2
= [(2 − ) − (1) ]
1
2 2
2
= 2 ∫ [(2 − ) − (1) ]
0
1
2
4
= 2 ∫ [3 + − 4 ]
0
2 1
4
= 2 [3 + − 4 ]
0
56
3
=
15
Método de Rebanadas

Suponga que V es el volumen del sólido mostrado en la Fig. 12 acotado por planos que son
perpendiculares al eje x en x=a y a=b. Además, suponga que conoce una función continua A(x) que

proporciona el área de una región de sección transversal que se forma al rebanar el sólido y un plano
perpendicular al eje x; en otras palabras, una rebanada es la intersección del sólido y un plano. Con esto

en mente, suponga que rebana al solido en cortes delgados por planos paralelos (semejantes a rebanadas
de pan de caja comercial) de modo que el grosor o ancho de una rebanada es “Delata”x1. Al usar

cilindros rectos para aproximar los volúmenes de estas rebanadas es posible construir una integral

definida que proporcione el volumen V del sólido [4].
Página 8 de 14