Page 83 - PORTAFOLIO SEGUNDO PARCIAL

= 2 ⇒ = √

Ya que necesitamos rotarlo alrededor de Y, como: y = x2 => x = √y

A= π , siendo R = √ entonces
2
2
ΔV = π (√y) Δy por la suma de Riemman, optenemos:
4
4 1 1
2 4
2
2
= ∫ = ∫ = { = (4 − 0 )
0 2 0 2
0
1
= (4 − 0 ) = 8
2
3
2
2
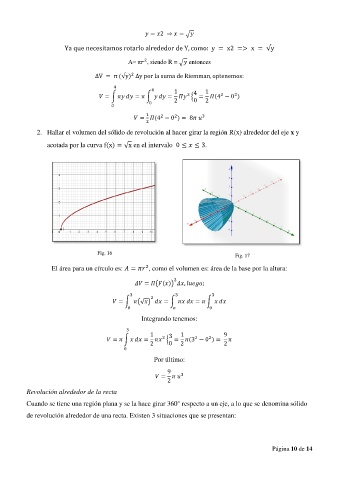
2. Hallar el volumen del sólido de revolución al hacer girar la región R(x) alrededor del eje x y
acotada por la curva f(x) = √x en el intervalo 0 ≤ ≤ 3.

Fig. 16 Fig. 17

2
El área para un círculo es: = , como el volumen es: área de la base por la altura:
2
= ( ( )) , ;
3 2 3 3
= ∫ (√ ) = ∫ = ∫
0 0
Integrando tenemos:

3
1 1 9
2 3
2
2
= ∫ = { = (3 − 0 ) =
2 0 2 2
0
Por último:
9
3
=
2
Revolución alrededor de la recta

Cuando se tiene una región plana y se la hace girar 360° respecto a un eje, a lo que se denomina sólido
de revolución alrededor de una recta. Existen 3 situaciones que se presentan:

Página 10 de 14