Page 26 - 20 Euclides

La paternidad de la Catóptrica es muy discutible. No obs-
tante, hay que poner de relieve que en ella se da una demostración
geométrica muy rigurosa de la ley de la reflexión de la luz. Esta ley
establece que los rayos de luz se reflejan según ángulos iguales
sobre la horizontal ( o sobre la vertical). Tomando la figura 1 como
guía, diríamos que el ángulo de incidencia 8 es igual al ángulo de
reflexión t. Para ello, Euclides se apoya en una proposición
geométrica que dice, en la versión incluida en el Libro I de los
Elementos:

------- Proposición 20. Dos lados de un
triángulo juntos son mayores que
FIG. 1
el tercer lado.
1
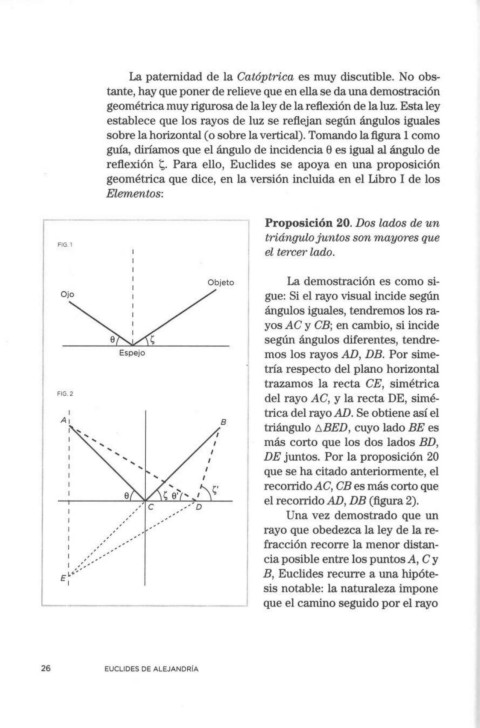
La demostración es como si-
o;~ ¡ /b;,to , gue: Si el rayo visual incide según
ángulos iguales, tendremos los ra-
~
yos AC y CE; en cambio, si incide
según ángulos diferentes, tendre-
Espejo mos los rayos AD, DE. Por sime-
tría respecto del plano horizontal
trazamos la recta CE, simétrica
FIG. 2
del rayo AC, y la recta DE, simé-
1 trica del rayo AD. Se obtiene así el
A1 B
triángulo 6.BED, cuyo lado BE es
más corto que los dos lados BD,
DE juntos. Por la proposición 20
que se ha citado anteriormente, el
recorrido AC, CE es más corto que
el recorrido AD, DE (figura 2).
,,' e
Una vez demostrado que un
rayo que obedezca la ley de la re-
fracción recorre la menor distan-
1 ,,::>•' cia posible entre los puntos A, C y
L•',, B, Euclides recurre a una hipóte-
El
sis notable: la naturaleza impone
que el camino seguido por el rayo

26 EUCLIDES DE ALEJANDRÍA