Page 91 - 11 Gauss

GAUSS Y SU CAMPANA
Gauss no fue el descubridor de la curva que lleva su nombre. La distribución
normal o curva de Gauss, como pasó a conocerse, también conocida por
campana de Gauss en estadística, fue presentada por primera vez por Abra-
ham de Moivre (1667-1754) en un artículo del año 1733, bastantes años antes
de que Gauss viera la luz. La función de densidad de una distribución normal
(que describe la probabilidad de que encontremos valores de la variable en
un determinado conjunto), que aparece de manera natural en el estudio del
comportamiento de fenómenos reales, es:
1 _(x-µ)'
f(x)---e 2o'
aJ2;,
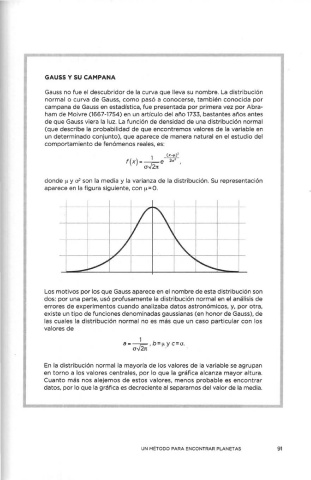
donde µ y 0 son la media y la varianza de la distribución. Su representación
2
aparece en la figura siguiente, con µ=O.

Los motivos por los que Gauss aparece en el nombre de esta distribución son
dos: por una parte, usó profusamente la distribución normal en el análisis de
errores de experimentos cuando analizaba datos astronómicos, y, por otra,
existe un tipo de funciones denominadas gaussianas (en honor de Gauss), de
las cuales la distribución normal no es más que un caso particular con los
valores de
1
a• -r::-, b=µ y c=o.
ov2rt · ·

En la distribución normal la mayoría de los valores de la variable se agrupan
en torno a los valores centrales, por lo que la gráfica alcanza mayor altura.
Cuanto más nos alejemos de estos valores, menos probable es encontrar
datos, por lo que la gráfica es decreciente al separarnos del valor de la media.

UN MÉTODO PARA ENCONTRAR PLANETAS 91