Page 52 - 15 Arquimedes
P. 52
UN GIGANTE SOBRE EL AGUA
El agua presenta una curiosa anomalía que es la razón, entre otras cosas, de
que puedan existir los océanos y la propia vida: en estado sólido es menos
densa que en estado líquido. Esto significa que un trozo de hielo puede flotar
libremente sobre el agua líquida. Es lo que ocurre, por ejemplo, con los ice-
bergs. La palabra iceberg proviene del neerlandés, a través del inglés, y sig-
nifica, literalmente, «témpano de hielo». Se trata de gigantescos pedazos de
hielo de agua dulce que quedan a la deriva en el océano y suelen ser arrastra-
dos a latitudes más bajas, por ejemplo, por la corriente del Labrador y la de
Groenlandia. Cuando un iceberg flota, lo hace hundiendo parte de su propio
volumen en el agua liquida. La razón dinámica es que se igualan así el peso
del iceberg (P) con el empuje (E) realizado por el agua liquida, el cual será
idéntico en número al peso del agua que cabe en el volumen ocupado por el
iceberg (V ) .
5
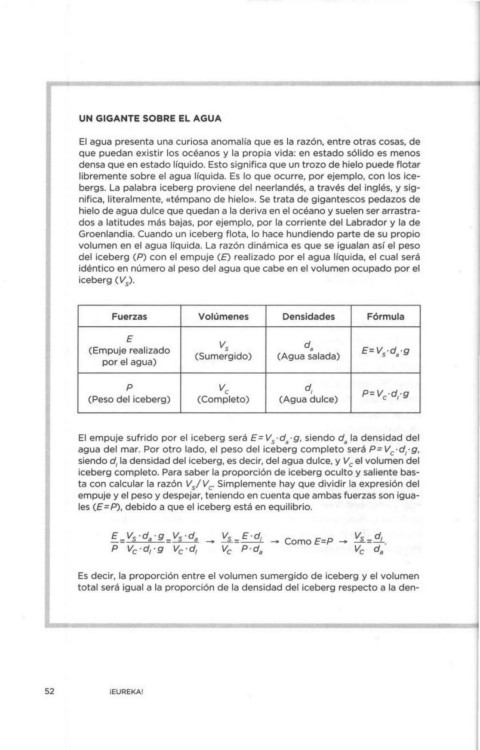
Fuerzas Volúmenes Densidades Fórmula
E
vs d.
(Empuje realizado E= V ·d. ·g
(Sumergido) (Agua salada) 5
por el agua)
p ve d,
(Peso del iceberg) (Completo) (Agua dulce) P=Ve· d,·g
El empuje sufrido por el iceberg será E= V · d g , siendo dª la densidad del
5 0
agua del mar. Por otro lado, el peso del iceberg completo será P =Ve· d, · g,
siendo d, la densidad del iceberg, es decir, del agua dulce, y Ve el volumen del
iceberg completo. Para saber la proporción de iceberg oculto y saliente bas-
ta con calcular la razón V / Vc Simplemente hay que dividir la expresión del
5
empuje y el peso y despejar, teniendo en cuenta que ambas fuerzas son igua-
les (E= P), debido a que el iceberg está en equilibrio.
5-= Vs ·da·g _ Vs ·da Vs = E . d, __,. Como E=P __,. Vs = d,
~ P·~ ~ ~
P Ve · d 1 · g Ve · d 1
Es decir, la proporción entre el volumen sumergido de iceberg y el volumen
total será igual a la proporción de la densidad del iceberg respecto a la den-
52 iEUREKA'