Page 32 - June

METALWORKING EQUIPMENT AND TOOLS

obtaining a high-quality surface of the machined part. First, when there is the disturbing effect
inherent in this technological operation, the deviation of the phase coordinate can be so great
that the subsequent manifestation of stable behavior (restoration of the relative position of the
tool and the workpiece) does not prevent the occurrence of defects on the surface. Secondly,
the absence stability, manifested in the relatively slow development of the deviation from the
initial position of the tool and workpiece, can be valid if a new change in cutting conditions
occurs before the deviation exceeds acceptable limits. Such changes occur, for example, in
the cycle of formation of chip elements, the release of which either loads the elastic system or
reduces the load.
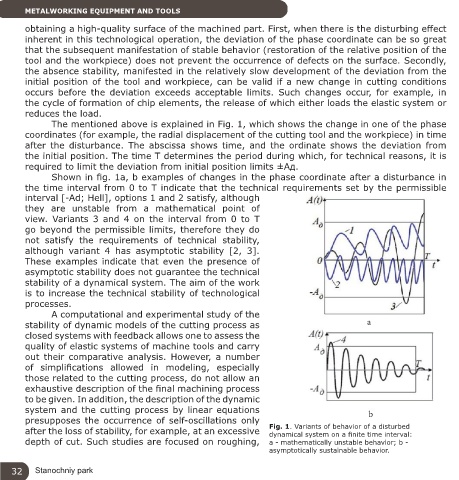
The mentioned above is explained in Fig. 1, which shows the change in one of the phase
coordinates (for example, the radial displacement of the cutting tool and the workpiece) in time
after the disturbance. The abscissa shows time, and the ordinate shows the deviation from
the initial position. The time T determines the period during which, for technical reasons, it is
required to limit the deviation from initial position limits ±Ад.
Shown in fig. 1a, b examples of changes in the phase coordinate after a disturbance in
the time interval from 0 to T indicate that the technical requirements set by the permissible
interval [-Ad; Hell], options 1 and 2 satisfy, although
they are unstable from a mathematical point of
view. Variants 3 and 4 on the interval from 0 to T
go beyond the permissible limits, therefore they do
not satisfy the requirements of technical stability,
although variant 4 has asymptotic stability [2, 3].
These examples indicate that even the presence of
asymptotic stability does not guarantee the technical
stability of a dynamical system. The aim of the work
is to increase the technical stability of technological
processes.
A computational and experimental study of the
stability of dynamic models of the cutting process as a
closed systems with feedback allows one to assess the
quality of elastic systems of machine tools and carry
out their comparative analysis. However, a number
of simplifications allowed in modeling, especially
those related to the cutting process, do not allow an
exhaustive description of the final machining process
to be given. In addition, the description of the dynamic
system and the cutting process by linear equations b
presupposes the occurrence of self-oscillations only
after the loss of stability, for example, at an excessive Fig. 1. Variants of behavior of a disturbed
dynamical system on a finite time interval:
depth of cut. Such studies are focused on roughing, a - mathematically unstable behavior; b -
asymptotically sustainable behavior.

32 Stanochniy park