Page 32 - Июнь

МЕТАЛЛООБРАБАТЫВАЮЩЕЕ ОБОРУДОВАНИЕ И ИНСТРУМЕНТ

точным условием получения качественной поверхности обработанной детали. Во-первых,
при возникновении возмущающего воздействия, свойственного данной технологической
операции, отклонение фазовой координаты может быть столь велико, что проявление в
дальнейшем устойчивого поведения (восстановление относительного положения инстру-
мента и заготовки) не спасает от возникновения дефектов на поверхности. Во-вторых,
отсутствие устойчивости, проявляющееся в сравнительно медленном развитии отклонения
от начального положения инструмента и заготовки, может быть допустимым, если новое
изменение условий резания произойдёт прежде, чем отклонение выйдет за допустимые
пределы. Такие изменения возникают, например, в цикле формирования элементов струж-
ки, выделение которых то нагружает упругую систему, то снижает нагрузку.
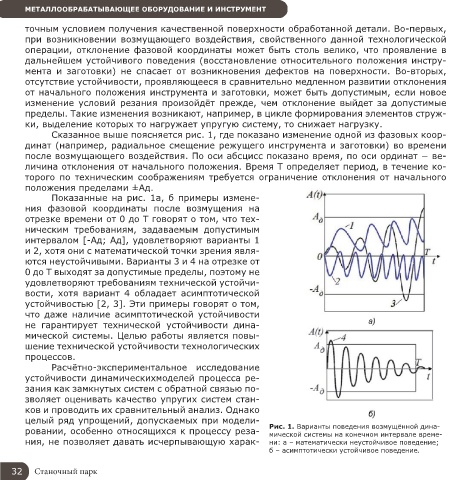
Сказанное выше поясняется рис. 1, где показано изменение одной из фазовых коор-
динат (например, радиальное смещение режущего инструмента и заготовки) во времени
после возмущающего воздействия. По оси абсцисс показано время, по оси ординат − ве-
личина отклонения от начального положения. Время Т определяет период, в течение ко-
торого по техническим соображениям требуется ограничение отклонения от начального
положения пределами ±Ад.
Показанные на рис. 1а, б примеры измене-
ния фазовой координаты после возмущения на
отрезке времени от 0 до Т говорят о том, что тех-
ническим требованиям, задаваемым допустимым
интервалом [-Ад; Ад], удовлетворяют варианты 1
и 2, хотя они с математической точки зрения явля-
ются неустойчивыми. Варианты 3 и 4 на отрезке от
0 до Т выходят за допустимые пределы, поэтому не
удовлетворяют требованиям технической устойчи-
вости, хотя вариант 4 обладает асимптотической
устойчивостью [2, 3]. Эти примеры говорят о том,
что даже наличие асимптотической устойчивости
не гарантирует технической устойчивости дина-
мической системы. Целью работы является повы-
шение технической устойчивости технологических
процессов.
Расчётно-экспериментальное исследование
устойчивости динамическихмоделей процесса ре-
зания как замкнутых систем с обратной связью по-
зволяет оценивать качество упругих систем стан-
ков и проводить их сравнительный анализ. Однако
целый ряд упрощений, допускаемых при модели-
ровании, особенно относящихся к процессу реза- Рис. 1. Варианты поведения возмущённой дина-
мической системы на конечном интервале време-
ния, не позволяет давать исчерпывающую харак- ни: а – математически неустойчивое поведение;
б – асимптотически устойчивое поведение.

32 Станочный парк