Page 117 - BUKU MATEMATIKA DASAR 1_Neat
P. 117
Penyelesaian :
Catat bahwa kontinu pada [0,1] dan terdiferensialkan pada (0,1) meskipun ada
1
suku 2. Karena (0) = 0 = (1), maka semua hipotesis dari teorema rolle
dipenuhi. Kemudian kita mencari turunan dari
1 1 2 1 1 1
−
−
′
( ) = 2 − 2 = 2(1 − 3 )
2 3 2
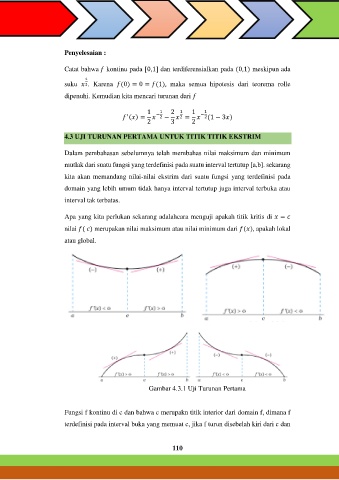
4.3 UJI TURUNAN PERTAMA UNTUK TITIK TITIK EKSTRIM
Dalam pembahasan sebelumnya telah membahas nilai maksimum dan minimum
mutlak dari suatu fungsi yang terdefinisi pada suatu interval tertutup [a,b]. sekarang
kita akan memandang nilai-nilai ekstrim dari suatu fungsi yang terdefinisi pada
domain yang lebih umum tidak hanya interval tertutup juga interval terbuka atau
interval tak terbatas.
Apa yang kita perlukan sekarang adalahcara menguji apakah titik kritis di =
nilai ( ) merupakan nilai maksimum atau nilai minimum dari ( ), apakah lokal
atau global.
Gambar 4.3.1 Uji Turunan Pertama
Fungsi f kontinu di c dan bahwa c merupakn titik interior dari domain f, dimana f
terdefinisi pada interval buka yang memuat c, jika f turun disebelah kiri dari c dan
110