Page 115 - BUKU MATEMATIKA DASAR 1_Neat

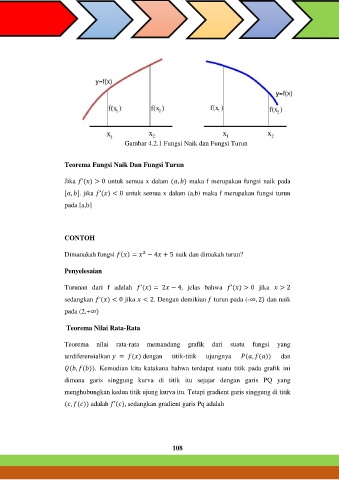
Gambar 4.2.1 Fungsi Naik dan Fungsi Turun

Teorema Fungsi Naik Dan Fungsi Turun

Jika ’( ) > 0 untuk semua x dalam ( , ) maka f merupakan fungsi naik pada

[ , ]. jika ’( ) < 0 untuk semua x dalam (a,b) maka f merupakan fungsi turun
pada [a,b]

CONTOH

2
Dimanakah fungsi ( ) = − 4 + 5 naik dan dimakah turun?

Penyelesaian

Turunan dari f adalah ’( ) = 2 − 4, jelas bahwa ’( ) > 0 jika > 2

sedangkan ’( ) < 0 jika < 2. Dengan demikian turun pada (-∞, 2) dan naik
pada (2,+∞)

Teorema Nilai Rata-Rata

Teorema nilai rata-rata memandang grafik dari suatu fungsi yang
terdiferensialkan = ( ) dengan titik-titik ujungnya ( , ( )) dan

( , ( )). Kemudian kita katakana bahwa terdapat suatu titik pada grafik ini
dimana garis singgung kurva di titik itu sejajar dengan garis PQ yang

menghubungkan kedua titik ujung kurva itu. Tetapi gradient garis singgung di titik

( , ( )) adalah ’( ), sedangkan gradient garis Pq adalah

108
