Page 110 - BUKU MATEMATIKA DASAR 1_Neat

 f ‘ (c) tidak ada.

CONTOH

1. Carilah nilai-nilai maksimum dan minimum dari

3
2
( ) = −2 + 3
1
Pada [− , 2]
2
Penyelesaian :

Mencari titik-titik kritis dari f .

1
Titik-titik ujung adalah − dan 2. Untuk mencari titik-titik stasioner kita selesaikan
2
′
2
, ( ) = −6 + 6 ,
→ −6 ( − 1) = 0

1
sehingga, untuk x diperoleh 0 dan 1. Jadi, titik-titik kritis adalah − , 0, 1, 2.
2
3 1 2
1
1
f (− ) = −2 (− ) + 3 (− ) = 1
2 2 2
3
(0) = −2(0) + 3(0) = 0
2
3
2
(1) = −2(1) + 3(1) = 1
2
3
(2) = −2(2) + 3(2) = - 4
1
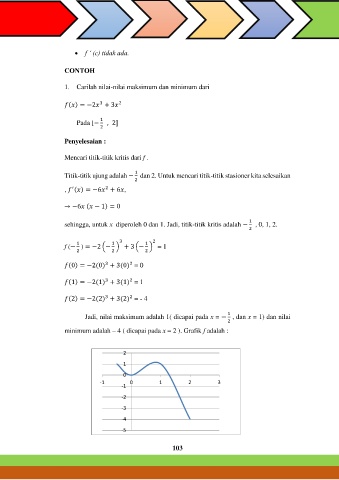
Jadi, nilai maksimum adalah 1( dicapai pada x = − , dan x = 1) dan nilai
2
minimum adalah – 4 ( dicapai pada x = 2 ). Grafik f adalah :

2
1

0
-1 0 1 2 3
-1
-2

-3

-4

-5

103
