Page 109 - BUKU MATEMATIKA DASAR 1_Neat

Dengan demikian, ekstrim local dari fungsi terdiferensialkan pada interval
buka dapat terjadi hanya disuatu titik dimana turunannya adalah nol, sehingga garis

singgung dari grafik di titik itu adalah horizontal.

4.1.3. MAKSIMUM DAN MINIMUM MUTLAK (GLOBAL)

y

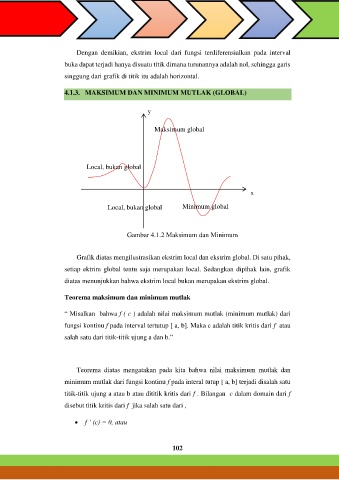
Maksimum global

Local, bukan global

x

Local, bukan global Minimum global

Gambar 4.1.2 Maksimum dan Minimum

Grafik diatas mengilustrasikan ekstrim local dan ekstrim global. Di satu pihak,
setiap ektrim global tentu saja merupakan local. Sedangkan dipihak lain, grafik

diatas menunjukkan bahwa ekstrim local bukan merupakan ekstrim global.

Teorema maksimum dan minimum mutlak

“ Misalkan bahwa f ( c ) adalah nilai maksimum mutlak (minimum mutlak) dari
fungsi kontinu f pada interval tertutup [ a, b]. Maka c adalah titik kritis dari f atau

salah satu dari titik-titik ujung a dan b.”

Teorema diatas mengatakan pada kita bahwa nilai maksimum mutlak dan

minimum mutlak dari fungsi kontinu f pada interal tutup [ a, b] terjadi disalah satu
titik-titik ujung a atau b atau dititik kritis dari f . Bilangan c dalam domain dari f

disebut titik kritis dari f jika salah satu dari ,

 f ‘ (c) = 0, atau

102
