Page 22 - 10A4

Å ã
b
N¸u a < 0 thì hàm sè đçng bi¸n trên kho£ng −∞; − và nghàch bi¸n trên
2a
b
Å ã
kho£ng − ; +∞ .
2a
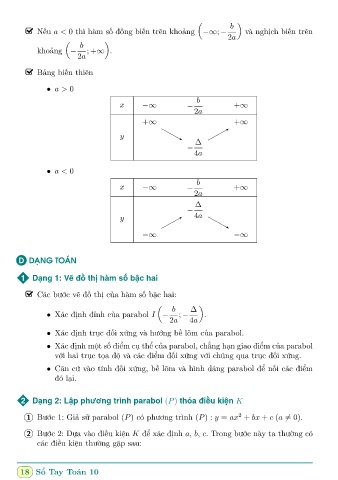
B£ng bi¸n thiên
• a > 0
b
x −∞ − +∞
2a
∞
+∞ +∞
∞
+
+
y
∆ ∆
− −
4a
4
a
• a < 0
b
x −∞ − +∞
2a
∆ ∆
− −
4
a
y 4a
−∞
−∞
−∞ −∞
D DẠNG TOÁN
1 Dạng 1: Vẽ đồ thị hàm số bậc hai
Các bưîc v³ đç thà cõa hàm sè bªc hai:
Å ã
b ∆
• Xác đành đ¿nh cõa parabol I − ; − .
2a 4a
• Xác đành tröc đèi xùng và hưîng b· lõm cõa parabol.
• Xác đành mët sè điºm cö thº cõa parabol, ch¯ng h¤n giao điºm cõa parabol
vîi hai tröc tåa đë và các điºm đèi xùng vîi chúng qua tröc đèi xùng.
• Căn cù vào tính đèi xùng, b· lõm và hình dáng parabol đº nèi các điºm
đó l¤i.

2 Dạng 2: Lập phương trình parabol (P) thỏa điều kiện K
2
1 Bưîc 1: Gi£ sû parabol (P) có phương trình (P) : y = ax + bx + c (a 6= 0).
2 Bưîc 2: Düa vào đi·u ki»n K đº xác đành a, b, c. Trong bưîc này ta thưíng có
các đi·u ki»n thưíng g°p sau:

18 Sê Tay Toán 10