Page 4 - UNI GEOMETRIA 5

Geometría 5° UNI

3. Si DF//AB y el triángulo DEF es equilátero,
20. Se ubica un punto E en la región interior del calcular el valor de .
triángulo ABC, tal que
AB = AE = EC, 2(m∢BCE) = m∢BAE.
Calcule la medida del ángulo entre AC y BE.

A) 30º B) 45º C) 60º
D) 90º E) 75º

=
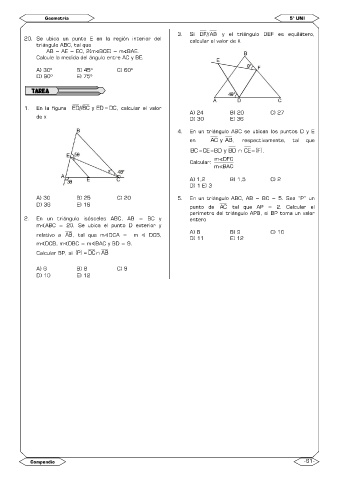
1. En la figura ED//BC y ED DC, calcular el valor
A) 24 B) 20 C) 27
de x D) 30 E) 36

4. En un triángulo ABC se ubican los puntos D y E
en AC y AB, respectivamente, tal que
BC CE BD y BD  CE=   F .
=
=
m DFC
Calcular:
m BAC

A) 1,2 B) 1,5 C) 2
D) 1 E) 3

A) 30 B) 25 C) 20 5. En un triángulo ABC, AB = BC = 5. Sea “P” un
D) 36 E) 18 punto de AC tal que AP = 2. Calcular el
perímetro del triángulo APB, si BP toma un valor
2. En un triángulo isósceles ABC, AB = BC y entero
mABC = 20. Se ubica el punto D exterior y
A) 8 B) 9 C) 10
relativo a AB, tal que mDCA = m  DCB,
D) 11 E) 12
mDCB, mDBC = mBAC y BD = 9.
Calcular BP, si   P = DC AB

A) 6 B) 8 C) 9
D) 10 E) 12

Compendio -61-