Page 5 - UNI GEOMETRIA 5

Geometría 5° UNI

26
Semana

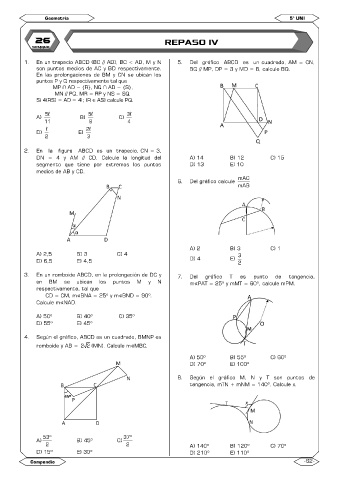
1. En un trapecio ABCD (BC // AD), BC < AD, M y N 5. Del gráfico ABCD es un cuadrado, AM = CN,
son puntos medios de AC y BD respectivamente. BQ // MP, DP = 3 y MD = 8, calcule BQ.
En las prolongaciones de BM y CN se ubican los
puntos P y Q respectivamente tal que
MP ∩ AD = {R}, NQ ∩ AD = {S},
MN // PQ, MR = RP y NS = SQ.
Si 4(RS) = AD = 4l; (R ∈ AS) calcule PQ.

A) 5l B) 5l C) 3l
11 8 4
D) l E) 2l
2 3

2. En la figura ABCD es un trapecio, CN = 3,
DN = 4 y AM // CD. Calcule la longitud del A) 14 B) 12 C) 15
segmento que tiene por extremos los puntos D) 13 E) 10
medios de AB y CD.
mAC
6. Del gráfico calcule
mAB

A) 2 B) 3 C) 1
A) 2,5 B) 3 C) 4 3
D) 6,5 E) 4,5 D) 4 E) 2

3. En un romboide ABCD, en la prolongación de DC y 7. Del gráfico T es punto de tangencia,
en BM se ubican los puntos M y N m∢PAT = 25º y mMT = 60º, calcule mPM.
respectivamente, tal que
CD = CM, m∢BNA = 25º y m∢BND = 90º.
Calcule m∢NAD.

A) 50º B) 40º C) 35º
D) 55º E) 45º

4. Según el gráfico, ABCD es un cuadrado, BMNP es
romboide y AB = 2 2 (MN). Calcule m∢MBC.

A) 50º B) 55º C) 60º
D) 70º E) 100º

8. Según el gráfico M, N y T son puntos de
tangencia, mTN + mNM = 140º. Calcule x.

53º 37º
A) B) 45º C)
2 2 A) 140º B) 120º C) 70º
D) 15º E) 30º D) 210º E) 110º

Compendio -62-