Page 23 - geometria

Geometría 5° Católica

16 RELACIÓN DE ÁREAS

Semana

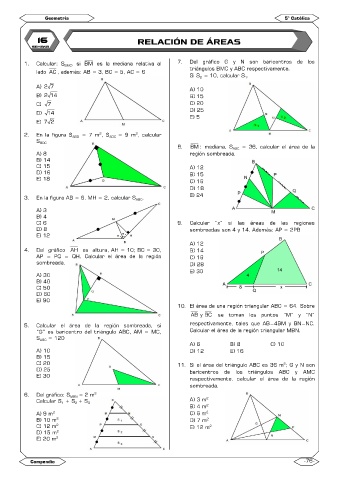
1. Calcular: S BMC , si BM es la mediana relativa al 7. Del gráfico G y N son baricentros de los
lado AC , además: AB = 3, BC = 5, AC = 6 triángulos BMC y ABC respectivamente.
Si S = 10, calcular S .
1
2
A) 2 7 A) 10
B) 2 14 B) 15
C) 7 C) 20
D) 14 D) 25
E) 5
E) 72

2
2
2. En la figura S ABD = 7 m , S ADC = 9 m , calcular
S BDC
8. BM : mediana, S ABC = 36, calcular el área de la
A) 8 región sombreada.
B) 14
C) 15 A) 12
D) 16 B) 15
E) 18 C) 16
D) 18

3. En la figura AB = 6, MH = 2, calcular S ABC . E) 24

A) 3
B) 4
C) 6 9. Calcular “x” si las áreas de las regiones
D) 8 sombreadas son 4 y 14. Además: AP = 2PB
E) 12
A) 12
4. Del gráfico AH es altura, AH = 10; BC = 30, B) 14
AP = PQ = QH. Calcular el área de la región C) 16
sombreada. D) 28
E) 30
A) 30
B) 40
C) 50
D) 60
E) 90
10. El área de una región triangular ABC = 64. Sobre
AB y BC se toman los puntos “M” y “N”

5. Calcular el área de la región sombreada, si respectivamente, tales que AB=4BM y BN=NC.
“G” es baricentro del triángulo ABC, AM = MC, Calcular el área de la región triangular MBN.
S ABC = 120
A) 6 B) 8 C) 10
A) 10 D) 12 E) 16
B) 15
C) 20 11. Si el área del triángulo ABC es 36 m ; G y N son
2
D) 25 baricentros de los triángulos ABC y AMC
E) 30 respectivamente, calcular el área de la región

sombreada.
6. Del gráfico: S MBN = 2 m
2
2
Calcular S + S + S A) 3 m
2
3
1
2
B) 4 m
2
2
A) 9 m C) 6 m
2
B) 10 m D) 7 m
2
C) 12 m E) 12 m
2
2
2
D) 15 m
E) 20 m
2

Compendio -76-