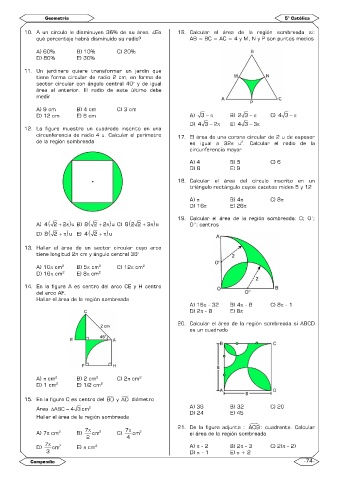
Page 21 - geometria
P. 21
Geometría 5° Católica
10. A un círculo le disminuyen 36% de su área. ¿En 16. Calcular el área de la región sombreada si:
qué porcentaje habrá disminuido su radio? AB = BC = AC = 4 y M, N y P son puntos medios
A) 60% B) 10% C) 20%
D) 80% E) 30%
11. Un jardinero quiere transformar un jardín que
tiene forma circular de radio 2 cm, en forma de
sector circular con ángulo central 40° y de igual
área al anterior. El radio de este último debe
medir
A) 9 cm B) 4 cm C) 3 cm
D) 12 cm E) 6 cm A) 3 − π B) 23 − π C) 4 3 − π
D) 4 3 − 2π E) 4 3 − 3π
12. La figura muestra un cuadrado inscrito en una
circunferencia de radio 4 u. Calcular el perímetro 17. El área de una corona circular de 2 u de espesor
de la región sombreada es igual a 32π u . Calcular el radio de la
2
circunferencia mayor
A) 4 B) 5 C) 6
D) 8 E) 9
18. Calcular el área del círculo inscrito en un
triángulo rectángulo cuyos catetos miden 5 y 12
A) π B) 4π C) 8π
D) 16π E) 26π
19. Calcular el área de la región sombreada: O; O’;
2
4
2
82 2 +π
8
A) ( 2 +π ) u B) ( 2 +π ) u C) ( 3 ) u O”: centros
D) ( 2 +π ) u E) ( 2 +π ) u
4
8
13. Hallar el área de un sector circular cuyo arco
tiene longitud 2π cm y ángulo central 36°
2
2
2
A) 10π cm B) 5π cm C) 12π cm
D) 16π cm E) 8π cm
2
2
14. En la figura A es centro del arco CE y H centro
del arco AF.
Hallar el área de la región sombreada
A) 16π - 32 B) 4π - 8 C) 8π - 1
D) 2π - 8 E) 8π
20. Calcular el área de la región sombreada si ABCD
es un cuadrado
2
2
2
A) π cm B) 2 cm C) 2π cm
D) 1 cm E) 1/2 cm
2
2
15. En la figura C es centro del BD y AD diámetro
Área ABC∆ = 4 3 cm A) 36 B) 32 C) 20
2
D) 24
E) 45
Hallar el área de la región sombreada
7π 7π 21. De la figura adjunta : AOB : cuadrante. Calcular
2
2
A) 7π cm B) cm C) cm el área de la región sombreada
2
2 4
7π
D) cm E) π cm A) π - 2 B) 2π - 3 C) 2(π - 2)
2
2
3 D) π - 1 E) π + 2
Compendio -74-