Page 15 - UNI M2 Geometria 5to sec

Geometría 5° UNI

5
Semana

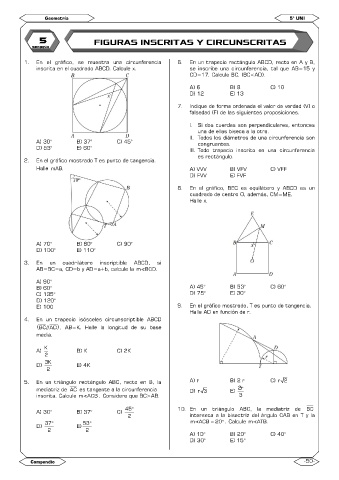
1. En el gráfico, se muestra una circunferencia 6. En un trapecio rectángulo ABCD, recto en A y B,
inscrita en el cuadrado ABCD. Calcule x. se inscribe una circunferencia, tal que AB=15 y
CD=17. Calcule BC. (BC<AD).

A) 6 B) 8 C) 10
D) 12 E) 13

7. Indique de forma ordenada el valor de verdad (V) o
falsedad (F) de las siguientes proposiciones.

I. Si dos cuerdas son perpendiculares, entonces
una de ellas biseca a la otra.
II. Todos los diámetros de una circunferencia son
A) 30° B) 37° C) 45° congruentes.
D) 53° E) 60° III. Todo trapecio inscrito en una circunferencia
es rectángulo.
2. En el gráfico mostrado T es punto de tangencia.
Halle mAB. A) VVV B) VFV C) VFF
D) FVV E) FVF

8. En el gráfico, BEC es equilátero y ABCD es un
cuadrado de centro O, además, CM=ME.
Halle x.

A) 70° B) 80° C) 90°
D) 100° E) 110°

3. En un cuadrilátero inscriptible ABCD, si
AB=BC=a, CD=b y AD=a+b, calcule la m BCD.

A) 90°
B) 60° A) 45° B) 53° C) 60°
C) 135° D) 75° E) 30°
D) 120°
E) 100 9. En el gráfico mostrado, T es punto de tangencia.
Halle AD en función de r.
4. En un trapecio isósceles circunscriptible ABCD
)
(BC//AD , AB=K. Halle la longitud de su base
media.

K
A) B) K C) 2K
2
3K
D) E) 4K
2

5. En un triángulo rectángulo ABC, recto en B, la A) r B) 2 r C) r 2
mediatriz de AC es tangente a la circunferencia D) r 3 E) 2r
inscrita. Calcule m ACB . Considere que BC>AB. 3

45  10. En un triángulo ABC, la mediatriz de BC
A) 30° B) 37° C)
2 interseca a la bisectriz del ángulo CAB en T y la
37  53  m = ACB  20 . Calcule m ATB.
D) E)
2 2
A) 10° B) 20° C) 40°
D) 30° E) 15°

Compendio -50-