Page 18 - UNI II M2 Álgebra
P. 18
Álgebra 5° UNI
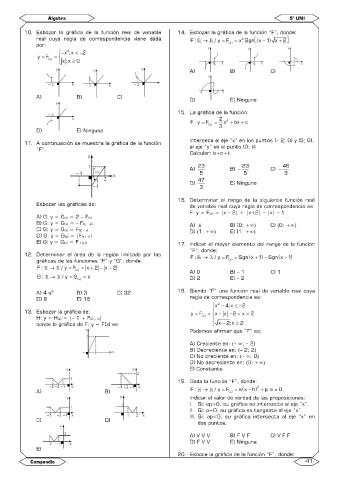
10. Esbozar la gráfica de la función real de variable 14. Esbozar la gráfica de la función “F”, donde:
real cuya regla de correspondencia viene dada F : → / y = F = x .Sgn 2 ( x 1− ) x + 2
por: ( ) x
2
− x ;x − 2
y = F ( ) x =
x ;x 0
A) B) C)
A) B) C)
D) E) Ninguno
15. La gráfica de la función:
2
2
F : y = F ( ) x = 3 x + bx +
c
D) E) Ninguna
11. A continuación se muestra la gráfica de la función Interseca al eje “x” en los puntos (– 2; 0) y (5; 0),
“F”. al eje “y” en el punto (0; k)
Calcular: b+c+k
23 23 46
A) B) − C) −
5 5 3
47
D) E) Ninguno
3
16. Determinar el rango de la siguiente función real
Esbozar las gráficas de: de variable real cuya regla de correspondencia es:
F: y = F(x) = |x – 2| + |x+2| – |x| – 1
A) G: y = G(x) = 2 – F(x)
B) G: y = G(x) = – F(x – 2) A) B) [0; +∞〉 C) 〈0; +∞〉
C) G: y = G(x) = F(2 – x) D) 〈1; +∞〉 E) [1; +∞〉
D) G: y = G(x) = |F(x+1)|
E) G: y = G(x) = F (|x|) 17. Indicar el mayor elemento del rango de la función
“F”, donde:
12. Determinar el área de la región limitada por las F : → / y = F = Sgn ( x + ) 1 − Sgn ( x 1− )
gráficas de las funciones “F” y “G”, donde: ( ) x
F : → / y = F ( ) x = x + 2 − x − 2 A) 0 B) – 1 C) 1
G : → / y = G ( ) x = x D) 2 E) – 2
2
A) 4 u B) 3 C) 32 18. Siendo “F” una función real de variable real cuya
D) 8 E) 16 regla de correspondencia es:
x − 4;x − 2
2
13. Esbozar la gráfica de: y = F = x − x ; 2 x 2
−
H: y = H(x) = |– 1 + F(2 – x)| ( ) x
donde la gráfica de F: y = F(x) es: x − 2;x 2
Podemos afirmar que “F” es:
A) Creciente en: 〈– ∞; – 2〉
B) Decreciente en: 〈– 2; 2〉
C) No creciente en: 〈– ∞; 0〉
D) No decreciente en: 〈0; +∞〉
E) Constante
19. Dada la función “F”, donde:
0
A) B) F : → / y = F ( ) x = a ( x − ) h 2 + p; a
Indicar el valor de verdad de las proposiciones:
I. Si: ap>0, su gráfica no intersecta al eje “x”.
II. Si: p=0, su gráfica es tangente al eje “x”.
III. Si: ap<0, su gráfica intersecta al eje “x” en
C) D)
dos puntos.
A) V V V B) F V F C) V F F
D) F V V E) Ninguna
E)
20. Esboce la gráfica de la función “F”, donde:
Compendio -41-