Page 3 - CAT III Geometria 5to SEC

Geometría 5° Católica

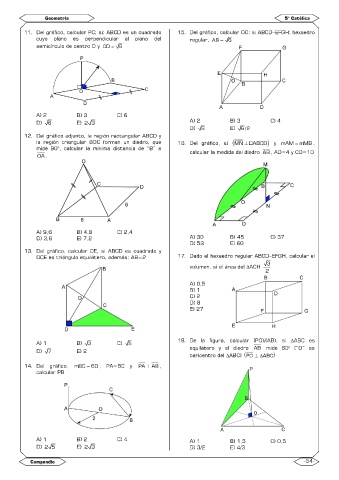
11. Del gráfico, calcular PC; si: ABCD es un cuadrado 15. Del gráfico, calcular OC: si ABCD–EFGH: hexaedro
cuyo plano es perpendicular al plano del regular, AB = 6
semicírculo de centro O y CD = 6

A) 2 B) 3 C) 6
D) 6 E) 2 3 A) 2 B) 3 C) 4
D) 6 E) 6/2
12. Del gráfico adjunto, la región rectangular ABCD y
la región triangular BOC forman un diedro, que 16. Del gráfico, si (MN ⊥ ABCD ) y mAM = mMB ,
mide 90°, calcular la mínima distancia de “B” a calcular la medida del diedro AB , AD=4 y CD=10
OA .

A) 9,6 B) 4,8 C) 2,4
D) 3,6 E) 7,2 A) 30 B) 45 C) 37
D) 53 E) 60
13. Del gráfico, calcular OE, si ABCD es cuadrado y
DCE es triángulo equilátero, además: AB=2 17. Dado el hexaedro regular ABCD–EFGH, calcular el
3
volumen, si el área del ACH
2

A) 0,5
B) 1
C) 2
D) 8
E) 27

A) 1 B) 3 C) 5 18. De la figura, calcular (PO)/(AB), si ABC es
D) 7 E) 2 equilátero y el diedro AB mide 60° (“O” es
baricentro del ABC) ( PO ⊥  ABC )
14. Del gráfico, mBC = 60 ; PA=BC y PA ⊥ AB ,
calcular PB

A) 1 B) 2 C) 4 A) 1 B) 1,5 C) 0,5
D) 2 5 E) 2 3 D) 3/2 E) 4/3

Compendio -54-