Page 21 - CAT M3 Geometría_Neat

Geometría 5° Católica

7
Semana

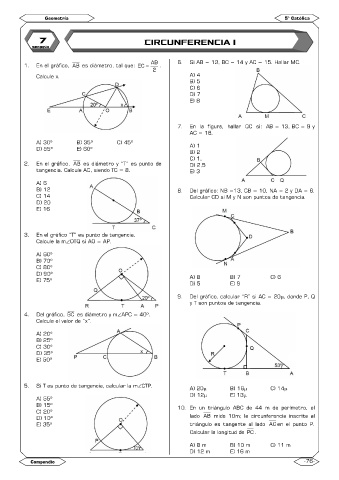
AB 6. Si AB = 13, BC = 14 y AC = 15. Hallar MC.
1. En el gráfico, AB es diámetro, tal que: EC = .
2
Calcule x. A) 4
B) 5
C) 6
D) 7
E) 8

7. En la figura, hallar QC si: AB = 13, BC = 9 y
AC = 18.

A) 30º B) 35º C) 45º
D) 55º E) 60º A) 1
B) 2
C) 1,
2. En el gráfico, AB es diámetro y “T” es punto de D) 2,5
tangencia. Calcule AC, siendo TC = 8. E) 3

A) 6
B) 12 8. Del gráfico: NB =13, CB = 10, NA = 2 y DA = 6.
C) 14 Calcular CD si M y N son puntos de tangencia.
D) 20
E) 16

3. En el gráfico “T” es punto de tangencia.
Calcule la mOTQ si AO = AP.

A) 60º
B) 70º
C) 80º
D) 90º A) 8 B) 7 C) 6
E) 75º
D) 5 E) 9
9. Del gráfico, calcular “R” si AC = 20, donde P, Q
y T son puntos de tangencia.

4. Del gráfico, BC es diámetro y mAPC = 40º.
Calcule el valor de “x”.

A) 20º
B) 25º
C) 30º
D) 35º
E) 50º

5. Si T es punto de tangencia, calcular la mCTP. A) 20 B) 16 C) 14
D) 12 E) 13
A) 55º
B) 15º 10. En un triángulo ABC de 44 m de perímetro, el
C) 20º
D) 10º lado AB mide 10m; la circunferencia inscrita al
E) 35º triángulo es tangente al lado AC en el punto P.
Calcular la longitud de PC .

A) 8 m B) 10 m C) 11 m
D) 12 m E) 16 m

Compendio -76-