Page 5 - CA GEOMETRIA 5

Geometría 5° Católica

26
Semana

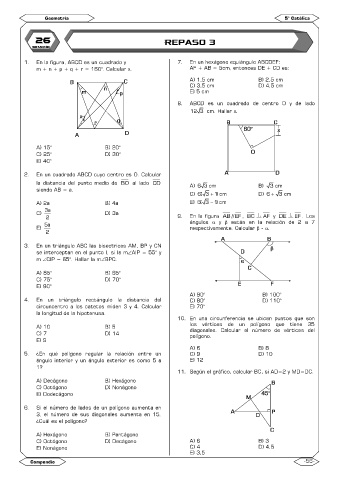
1. En la figura, ABCD es un cuadrado y 7. En un hexágono equiángulo ABCDEF:
m + n + p + q + r = 160°. Calcular x. AF + AB = 5cm, entonces DE + CD es:

A) 1,5 cm B) 2,5 cm
C) 3,5 cm D) 4,5 cm
E) 5 cm

8. ABCD es un cuadrado de centro O y de lado
12 3 cm. Hallar x.

A) 15° B) 20°
C) 25° D) 30°
E) 40°

2. En un cuadrado ABCD cuyo centro es O. Calcular

la distancia del punto medio de BO al lado CD A) 6 3 cm B) 3 cm
siendo AB = a.
C) 6( 3 + 1 ) cm D) 6 + 3 cm
A) 2a B) 4a E) 6( 3 − 1 ) cm
3a
C) D) 3a
2 9. En la figura AB //EF , BC AF y DE EF . Los
5a ángulos  y  están en la relación de 2 a 7
E) respectivamente. Calcular  - .
2

3. En un triángulo ABC las bisectrices AM, BP y CN
se interceptan en el punto I, si la mAIP = 55° y
m CIP = 65°. Hallar la mBPC.

A) 85° B) 65°
C) 75° D) 70°
E) 80°
A) 90° B) 100°
4. En un triángulo rectángulo la distancia del C) 80° D) 110°
circuncentro a los catetos miden 3 y 4. Calcular E) 70°
la longitud de la hipotenusa.
10. En una circunferencia se ubican puntos que son
A) 10 B) 5 los vértices de un polígono que tiene 35
diagonales. Calcular el número de vértices del
C) 7 D) 14 polígono.
E) 9
A) 6 B) 8
5. ¿En qué polígono regular la relación entre un C) 9 D) 10
ángulo interior y un ángulo exterior es como 5 a E) 12
1?
11. Según el gráfico, calcular BC, si AD=2 y MD=DC.

A) Decágono B) Hexágono
C) Octógono D) Nonágono
E) Dodecágono

6. Si el número de lados de un polígono aumenta en
3, el número de sus diagonales aumenta en 15.
¿Cuál es el polígono?

A) Hexágono B) Pentágono
C) Octógono D) Decágono A) 6 B) 3
E) Nonágono C) 4 D) 4,5
E) 3,5
Compendio -56-