Page 31 - MATERI AJAR E-MODUL KALKULUS-1_Neat

Jika dan fungsi serta ∩ ≠ ∅, maka terdapat suatu fungsi ℎ dari himpunan bagian
ke himpunan bagian yang disebut fungsi komposisi dan (ditulis ∘ ) yang
ditentukan dengan

ℎ( ) = ( ∘ )( ) = ( ( ))

Daerah asal fungsi komposisi dan adalah ∘ = { ∈ | ( ) ∈ }, dengan = daerah
asal (domain) fungsi ; = daerah asal (domain) fungsi ; = daerah hasil (range) fungsi
; = daerah hasil (range) fungsi .

1. Syarat Dua Fungsi Komposisi Ada

Ayo Menggali Informasi

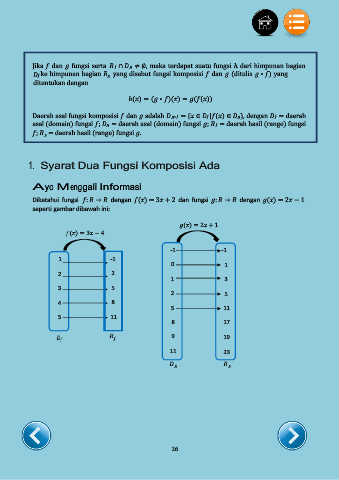
Diketahui fungsi : → dengan ( ) = 3 + 2 dan fungsi : → dengan ( ) = 2 − 1
seperti gambar dibawah ini:

( ) = 2 + 1
( ) = 3 − 4

-1 -1

1 -1
0 1

2 2
1 3

3 5
2 5

4 8
5 11

5 11
8 17

9
19

11 23

26