Page 32 - ASTRONOMI DAN ASTROFISIKA

matematis dapat kita nyatakan sebagai jumlah vektor perpindahan O dengan
Q
vektor perpindahan Q . Karena hasil perpindahan OQP sama dengan vektor
P
perpindahan PO , ini dapat dituliskan

O P = QO + PQ

Sekarang mari kita tuliskan PO = c , QO = a , dan PQ = b .

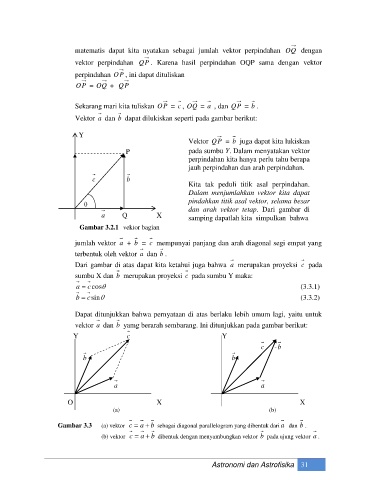
Vektor a dan b dapat dilukiskan seperti pada gambar berikut:

Y
Vektor PQ = b juga dapat kita lukiskan
P pada sumbu Y. Dalam menyatakan vektor
perpindahan kita hanya perlu tahu berapa
jauh perpindahan dan arah perpindahan.

c b
Kita tak peduli titik asal perpindahan.
Dalam menjumlahkan vektor kita dapat
θ pindahkan titik asal vektor, selama besar
dan arah vektor tetap. Dari gambar di
a Q X samping dapatlah kita simpulkan bahwa
Gambar 3.2.1 vektor bagian

jumlah vektor a + b = c mempunyai panjang dan arah diagonal segi empat yang

terbentuk oleh vektor a dan b .
Dari gambar di atas dapat kita ketahui juga bahwa a merupakan proyeksi c pada
sumbu X dan b merupakan proyeksi c pada sumbu Y maka:
a  c cos  (3.3.1)
b  c sin  (3.3.2)

Dapat ditunjukkan bahwa pernyataan di atas berlaku lebih umum lagi, yaitu untuk
vektor a dan b yamg berarah sembarang. Ini ditunjukkan pada gambar berikut:
Y c Y

c -b
b b

a a

O X X
(a) (b)

Gambar 3.3 (a) vektor c  a  b sebagai diagonal parallelogram yang dibentuk dari a dan b .
(b) vektor c  a  b dibentuk dengan menyambungkan vektor b pada ujung vektor a .
VEKTOR LAWAN

Astronomi dan Astrofisika 31