Page 40 - HS 8 Afgeleiden

P. 40

GeoGebra in de derde graad

8 Stelling van Rolle en Lagrange

8.7 De stelling van Rolle

8.7.1 Inleiding

f : ℝ → ℝ ; x → f(x)
Domein = D

[a, b] ⊆ D ⊆ = deelverzameling van of gelijk aan …
a ≠ b

Indien f continu is in [a, b]
f afleidbaar is in ]a, b[

f(a) = f(b)
Dan ∃ c ∈ ]a, b[ ; f’ (c) = 0 ∃ = er bestaat

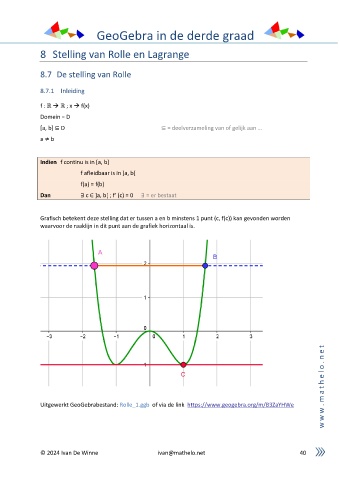
Grafisch betekent deze stelling dat er tussen a en b minstens 1 punt (c, f(c)) kan gevonden worden
waarvoor de raaklijn in dit punt aan de grafiek horizontaal is.

t
e
n
.
o
l
e
h
t
a
m
Uitgewerkt GeoGebrabestand: Rolle_1.ggb of via de link https://www.geogebra.org/m/B3ZaYHWe .
w
w

35 36 37 38 39 40 41 42 43 44 45