Page 12 - HS 7 De normale verdeling
P. 12
Combinatieleer, kansrekening en verklarende statistiek
7.4 Kenmerken van de normale verdeling
7.4.1 De standaardnormale verdeling met μ = 1 en σ = 0
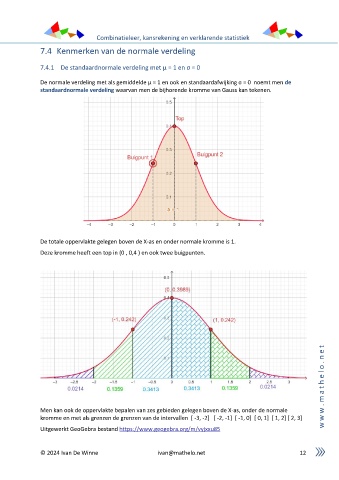
De normale verdeling met als gemiddelde μ = 1 en ook en standaardafwijking σ = 0 noemt men de
standaardnormale verdeling waarvan men de bijhorende kromme van Gauss kan tekenen.
De totale oppervlakte gelegen boven de X-as en onder normale kromme is 1.
Deze kromme heeft een top in (0 , 0,4 ) en ook twee buigpunten.
t
e
n
.
o
l
e
h
t
a
m
.
Men kan ook de oppervlakte bepalen van zes gebieden gelegen boven de X-as, onder de normale w
kromme en met als grenzen de grenzen van de intervallen [ -3, -2] [ -2, -1] [ -1, 0] [ 0, 1] [ 1, 2] [ 2, 3] w
w
Uitgewerkt GeoGebra bestand https://www.geogebra.org/m/vyjxxu85
© 2024 Ivan De Winne ivan@mathelo.net 12