Page 13 - HS 7 De normale verdeling

Combinatieleer, kansrekening en verklarende statistiek

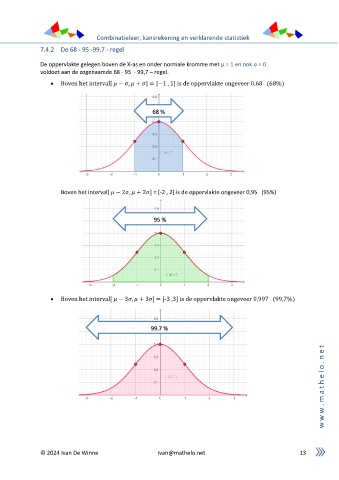
7.4.2 De 68 - 95 -99,7 - regel

De oppervlakte gelegen boven de X-as en onder normale kromme met μ = 1 en ook σ = 0
voldoet aan de zogenaamde 68 - 95 - 99,7 – regel.

• Boven het interval[ − , + ] = [−1 , 1] is de oppervlakte ongeveer 0,68 (68%)

68 %

Boven het interval[ − 2 , + 2 ] = [-2 , 2] is de oppervlakte ongeveer 0,95 (95%)

95 %

• Boven het interval[ − 3 , + 3 ] = [-3 ,3] is de oppervlakte ongeveer 0,997 (99,7%)

99,7 %

t
e
n
.
o
l
e
h
t
a
m
.

w
w
w

© 2024 Ivan De Winne ivan@mathelo.net 13