Page 14 - HS 7 De normale verdeling

Combinatieleer, kansrekening en verklarende statistiek

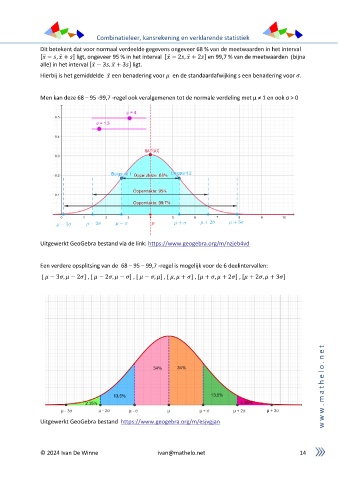
Dit betekent dat voor normaal verdeelde gegevens ongeveer 68 % van de meetwaarden in het interval
[ ̅ − , ̅ + ] ligt, ongeveer 95 % in het interval [ ̅ − 2 , ̅ + 2 ] en 99,7 % van de meetwaarden (bijna
̅
̅
alle) in het interval [ − 3 , + 3 ] ligt.
̅
Hierbij is het gemiddelde een benadering voor en de standaardafwijking s een benadering voor .

Men kan deze 68 – 95 -99,7 -regel ook veralgemenen tot de normale verdeling met μ ≠ 1 en ook σ > 0

Uitgewerkt GeoGebra bestand via de link: https://www.geogebra.org/m/nzjeb4vd

Een verdere opsplitsing van de 68 – 95 – 99,7 -regel is mogelijk voor de 6 deelintervallen:
[ − 3 , − 2 ] , [ − 2 , − ] , [ − , ] , [ , + ] , [ + , + 2 ] , [ + 2 , + 3 ]

t
e
n
.
o
l
e
h
t
a
m
.
w
w
Uitgewerkt GeoGebra bestand https://www.geogebra.org/m/esjvgjan
w

© 2024 Ivan De Winne ivan@mathelo.net 14