Page 22 - 수학(하)

B =
n A + g
] g
3) n A - g n A - ] B = 1 U
]
A B
오른쪽 그림과 같이 전체집합 U 를 각각 4 개의 영역으로 나누고 각각의
영역에 해당하는 원소의 개수를 1 , 2 , 3 , 4 라 하면 1 2 3
B =
n U = 1 + 2 + 3 + 4 에서 n A - g 1 이다. 4
]
]g
유형
C
C
예 전체집합 U 의 두 부분집합 ,AB 에 대하여 n U = 60 , n A = 40 , n B = 30 , n A + B g = 15 일 때, 01
]
] g
] g
] g
n A - Bg 를 구해 보자. 집
]
n U = 1 + 2 + 3 + 4 = 60 , n A = 1 + 2 = 40 , n B = 2 + 3 = 30 , 합
] g
] g
] g
n A ,
C
C
n A + B = ]] Bg g = 4 = 15 이므로
C
g
]
h
h
2 = ^ 1 + 2 + ^h 2 + 3 + 4 - ^ 1 + 2 + 3 + 4 = 40 + 30 + 15 - 60 = 25 이다.
B =
h
따라서 n A - g 1 = ^ 1 + 2 - 2 = 40 - 25 = 15 이다.
]
예 전체 학생 200 명 중에서 방과 후 수업으로 중국어를 신청한 학생이 120 명, 일본어를 신청한 학생이 115 명,
두 과목을 모두 신청하지 않은 학생은 20 명이다. 이 전체 학생 200 명 중에서 중국어만을 신청한 학생의
수를 구해 보자.
중국어와 일본어를 신청한 학생들의 집합을 각각 ,AB 라 하면
n U = 1 + 2 + 3 + 4 = 200 명 , n A = 1 + 2 = 120 명 , n B = 2 + 3 = 115명 ,
] g
] g
] g
n A ,
n A + B = ]] Bg g = 4 = 20 명이므로
C
C
C
]
g
2 = ^ 1 + 2 + ^h 2 + 3 + 4 - ^ 1 + 2 + 3 + 4 = 120 + 115 + 20 - 200 = 55 명이다.
h
h
B =
h
따라서 n A - g 1 = ^ 1 + 2 - 2 = 120 - 55 = 65 명이다.
]
4) n A , B , C = n A + ]g n B + ] g n A + B - ]g n B + C - ]g n C + A + ]g n A + B + Cg
g
]
n C - ]
g
]
U
= 1 + 2 + 3 + 4 + 5 + 6 + 7
A B
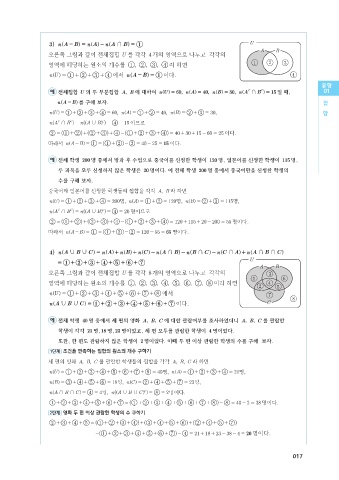
오른쪽 그림과 같이 전체집합 U 를 각각 8 개의 영역으로 나누고 각각의 3
1 6
영역에 해당하는 원소의 개수를 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 이라 하면 4
2 5
n U = 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 에서 7
]g
8
n A , B , C = 1 + 2 + 3 + 4 + 5 + 6 + 7 이다. C
]
g
,
,
예 전체 학생 40 명 중에서 세 편의 영화 ,AB C 에 대한 관람여부를 조사하였더니 ,AB C 를 관람한
학생이 각각 21 명, 18 명, 23 명이었고, 세 편 모두를 관람한 학생이 4 명이었다.
또한, 한 편도 관람하지 않은 학생이 2 명이었다. 이때 두 편 이상 관람한 학생의 수를 구해 보자.
1단계 조건을 만족하는 집합의 원소의 개수 구하기
,
,
세 편의 영화 ,AB C 를 관람한 학생들의 집합을 각각 ,AB C 라 하면
n U = 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 = 40 명 , n A = 1 + 2 + 3 + 4 = 21 명 ,
] g
] g
n B = 3 + 4 + 5 + 6 = 18 명 , n C = 2 + 4 + 5 + 7 = 23 명 ,
] g
] g
n A + B + g 4 = 4 명 , n A , B , Cg g = 8 = 2 명 이다.
C =
C
]
]]
1 + 2 + 3 + 4 + 5 + 6 + 7 = ^ 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 - 8 = 40 - 2 = 38 명이다.
h
2단계 영화 두 편 이상 관람한 학생의 수 구하기
2 + 3 + 4 + 5 = ^ 1 + 2 + 3 + 4 + ^h 3 + 4 + 5 + 6 + ^h 2 + 4 + 5 + 7 h
h
-^ 1 + 2 + 3 + 4 + 5 + 6 + 7 - 4 = 21 + 18 + 23 - 38 - 4 = 20 명이다.
017