Page 53 - POSTER FYP MAC-OGOS 2025

NAME: MARYAM BASYIRAH BINTI ZULKIFLI (2023115083) (K242/54)

SUPERVISOR: NORLAILA BINTI MD NOR

Abstract

In this study, SEIR model is developed for the transmission of measles to analyze the stability of disease-free and endemic equilibrium points and to evaluate

how varying testing and therapy rates (σ) and contact rates (β) affect measles spread. The model equations were solved numerically, and parameter values

were adopted from different previous studies. Simulations were performed using Maple software to analyze the impact of different values of σ and β on the

infectious, and recovered populations. The results show that the disease-free equilibrium is stable when the eigenvalues is less than zero, indicating potential

for eradication, and a zero eigenvalue at the endemic equilibrium indicates that measles may persist at a stable level. The simulation shows that increase in

the testing and therapy rates can increase the recovered population while decrease the infectious population. On the contrary, increase in contact rates lead to

an increase in the infectious population. These results show that early testing and treatment and the need to minimize contact rates are important.

Problem Statement Objectives

The increase in the number of measles globally which has become public concern, also To conduct stability analysis of the SEIR model by

take place in European region. Since 2016, large measles outbreak has occurred in one of computing and classifying disease-free and endemic

the European countries, which is Romania. Among the countries in European region, equilibrium points.

Romania was reported to achieve the highest number of measles cases. Although the To analyze the impact of varying testing and therapy (σ)

previous study by Sowole et al. (2019) investigated on the existence, stability, and and contact rate (β) on measles transmission dynamics

uniqueness of the SEIR model, it focused more on theory analysis rather than applied the by conducting numerical simulations.

model to actual data.

Methodology & Implementation Results & Discussion

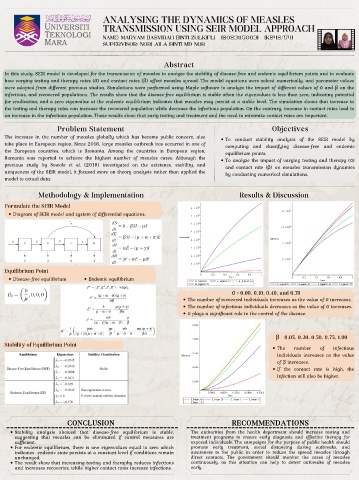
Formulate the SEIR Model

Diagram of SEIR model and system of differential equations.

Equilibrium Point

Disease-free equilibrium Endemic equilibrium

σ = 0.00, 0.10, 0.40, and 0.70

The number of recovered individuals increases as the value of σ increases.

The number of infectious individuals decreases as the value of σ increases.

σ plays a significant role in the control of the disease.

β = 0.05, 0.20, 0.50, 0.75, 1.00

Stability of Equilibrium Point

The number of infectious

individuals increases as the value

of β increases.

If the contact rate is high, the

infection will also be higher.

CONCLUSION RECOMMENDATIONS

Stability analysis showed that disease-free equilibrium is stable, The authorities from the health department should increase testing and

suggesting that measles can be eliminated if control measures are treatment programs to ensure early diagnosis and effective therapy for

sufficient. exposed individuals. The campaigns for the purpose of public health should

For endemic equilibrium, there is one eigenvalues equal to zero which promote early treatment, social distancing during outbreaks, and

indicates endemic state persists at a constant level if conditions remain awareness to the public in order to reduce the spread measles through

unchanged. direct contacts. The government should monitor the cases of measles

The result show that increasing testing and theraphy reduces infections continuously, as this situation can help to detect outbreaks of measles

and increases recoveries, while higher contact rates increase infections. early.