Page 458 - Álgebra

COLECCIÓN ESENCIAL Lumbreras Editores

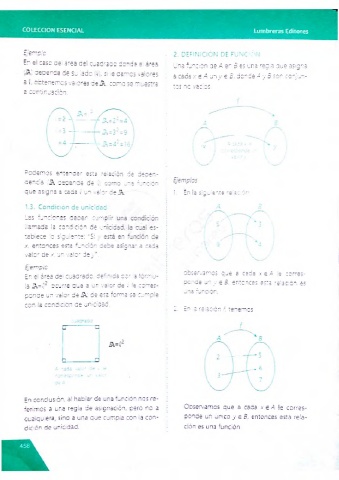
E je m p lo : ¡ o *
-n si caso de! ¿rea de cuadrado donde el ¿rea Una función de A en S es una regía que asiona

(Ik ) depende de su ¡acó (X), si !e damos valores
a caca ,r e A un y e 5, donde A y 8 son conjun­
a i, obtenemos valores de I k , como se muestra
tos no vacíos.
a continuación.

Podemos entender- esta relace ■ ae óepe.o-
denos {I k depende oe f) cerne u.na fundón
oue ssíona a cada £ur, valor ce i I. En a siauiente relación:

-1
Las fuñe-1U oes dsben cl rr
llamada la cono!icíón C£ U:
tablees lo siguie c - “Si y ■
a
i
t>

n
e
e
x , enton s esta fu n c en dteee asmnar a cao:
valor de X, un val:or esr Vf
E je m p lo
oeservamos oue a caca x s A le corres­
En el ares del cuadrado, definida por la fórma­
ponde un y e S , entonces esta relación es

la l k = r , ocurre que a un valor oe £íe corres­
una función.
ponde un valor de J k de esa rernta se curre f
con Is condición de unicidad.
2. En ia relación f tenemos
G □

I

n _____ri

En conclusión, a! hablar de un3 función nos re­
ferimos a una regia ce asignación, pero no a Observamos que a cada x e A le corres­
cuaiquiera, sino a una que cumpla con la con­ ponde un único y e 8 , entonces esta rela­
dición ríe unicidad. ción es una función.